OpenCASCADE Conic to BSpline Curves-Parabola
Abstract. Rational Bezier Curve can represent conic curves such as circle, ellipse, hyperbola, .etc. But how to convert a conic curve to BSpline curve is still question, i.e. Represent a conic curve in BSpline form. Parabola curve is the most simple conic curve, that the parabola does not require rational functions. Let’s begin from the simplest one…
Key Words. OpenCASCADE, Convert, Parabola, BSplineCurve, Conic Curve
1. Introduction
圆锥截线(Conic或称为二次曲线)和圆在CAD/CAM中有着广泛应用。毫无疑问NURBS的一个最大优点就是既能精确表示圆锥截线和圆,也能精确表示自由曲线曲面。这个优点的意义是方便编程,使所有的曲线可以采用统一的数据结构来表示。通过有理的方式可以精确来表示这些二次曲线,那么给定一个二次曲线的相关参数(如圆的圆心和半径等),如何构造出对应的NURBS曲线呢?
在圆锥截线中,抛物线(Parabola)是不需要用有理函数来表示的,所以是形式最简单的二次曲线。先从简单的着手,来学习如何将一个抛物线从隐式方程的形式转换成NURBS曲线形式。
先简要回顾一下高中数学中关于抛物线的相关知识点,如下图所示为我上高中时数学课本中的关于抛物线方程及焦点坐标(focus)和准线(directrix)方程一个图表:
Figure 1.1 Parabola Fuction
OpenCASCADE中对应抛物线的隐式方程表示的类是gp_Parab/gp_Parab2d。本文主要介绍OpenCASCADE中如何将gp_Parab2d转换为NURBS曲线。
2. Parametric Representations
在CAD/CAM的应用中,圆锥截线有两种重要的参数表示形式:有理形式和最大内接面积形式(Rational and maximum inscribed area forms)。表示抛物线的这两种形式是相同的,如下所示:
圆锥截线的有些有理参数表示形式可能是有相当差的参数化,即均匀分布的参数值对应于曲线上分布很不均匀的点。利用线性有理函数对有理曲线进行重新参数化可以改变(因而可能改善)其参数化。
假设C(u)=(x(u), y(u))是一条在标准位置的圆锥截线的参数表示。现在我们对抛物线给出的参数方程也是上式,它是一个好的参数化:对于任意给定的整数n和参数边界a与b,取n个等间隔分布的参数:
点C(u1),C(u2), …, C(un)形成曲线上n-1边多边形,它的闭合多边形具有最大的内接面积。
根据最大内接面积表示法可以求出节点矢量。
3. Conversion Algorithm
将隐式表示的抛物线方程转换为NURBS(有理Bezier是NURBS的特例)曲线需要确定NURBS的以下信息:节点矢量,权因子,次数,控制顶点。
因为抛物线是二次曲线,所以对应的NURBS曲线的次数也为2。因为是用有理的Bezier曲线来表示的,所以需要的控制顶点数为3。
其中节点矢量可由最大内接面积表示法来确定。下面来确定剩余的所需数据。由有理Bezier曲线的公式得二次有理Bezier曲线弧的表示形式为:
称k为形状不变因子,公式如下所示:
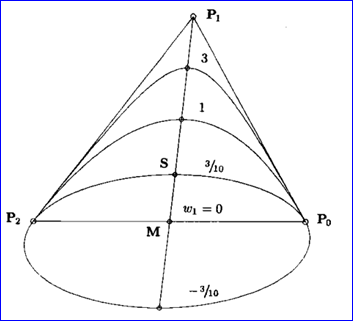
可以证明同一组控制顶点选取不同 的权因子,只要形状因子k相等,则由它们决定的二次有理Bezier曲线是同一条曲线段,不同的权因对应不同的参数化,而且可以根据形状不变因子对二次曲线进行分类:
v K=0; 表示退化的二次曲线:一对直线段P0P1和P1P2;
v K∈[0,1]; 表示双曲线;
v K=1; 表示抛物线;
v K∈[1, +∞]; 表示椭圆;
v K=+∞; 表示连接P0和P2的直线段;
习惯上我们选择ω0=ω2=1称为标准参数化。此时由形状因子k公式得抛物线的ω1=1。所以抛物线的权因子也因此而确定,即ω0=ω1=ω2=1。
Figure 3.1 不同的权因子ω1 定义的圆锥截线
由二次有理Bezier曲线公式可知,当u=0和u=1时,C(0)=P0, C(1)=P2,即曲线通过特征多边形的首末顶点。由此可确定抛物线的两个控制顶点P0和P2,现在只剩下最后一个P1顶点未确定。
P1点可以由二次有理Bezier曲线的公式列方程计算得出,但这并不是一个方便的方法。一种更方便的方法是:在这条曲线上指定第三个点,该点对应于某个特定的参数,例如u=1/2。点S=C(1/2)称为圆锥截线的肩点(shoulder point),如图3.1所示。将u=1/2代入二次有理Bezier公式得:
其中M是弦P0P2的中点。肩点S=C(1/2)。所以由上式可确定P1点。下面将各个控制顶点的计算列出如下所示:
设抛物线的起止区间为[UF,UL],则因为曲线通过特征多边形的顶点,所以通过首点P0=(X0,Y0)=(X0,UF)。又由抛物线的参数方程可知:
同理可计算出通过末点P2的坐标,将他们分别列出如下:
由计算肩点S的公式,将Sy=Y1=C(u1)=(UF+UL)/2代入可得:
所以P1点的坐标为:
至此,抛物线的三个控制顶点P0,P1,P2都已计算出来了。即抛物线的NURBS表示所需的数据都已经得到了。下面看看OpenCASCADE中的实现代码。
4. Code Analysis
OpenCASCADE的Math工具集中有个包Covert用来将圆锥曲线曲面转换为NURBS曲线曲面。其中转换抛物线的类为:Convert_ParabolaToBSplineCurve,实现代码如下所示:
//======================================================================= //function : Convert_ParabolaToBSplineCurve //purpose : //======================================================================= Convert_ParabolaToBSplineCurve::Convert_ParabolaToBSplineCurve (const gp_Parab2d& Prb, const Standard_Real U1 , const Standard_Real U2 ) : Convert_ConicToBSplineCurve (MaxNbPoles, MaxNbKnots, TheDegree) { Standard_DomainError_Raise_if( Abs(U2 - U1) < Epsilon(0.), \"Convert_ParabolaToBSplineCurve\"); Standard_Real UF = Min (U1, U2); Standard_Real UL = Max( U1, U2); Standard_Real p = Prb.Parameter(); nbPoles = 3; nbKnots = 2; isperiodic = Standard_False; knots->ChangeArray1()(1) = UF; mults->ChangeArray1()(1) = 3; knots->ChangeArray1()(2) = UL; mults->ChangeArray1()(2) = 3; weights->ChangeArray1()(1) = 1.; weights->ChangeArray1()(2) = 1.; weights->ChangeArray1()(3) = 1.; gp_Dir2d Ox = Prb.Axis().XDirection(); gp_Dir2d Oy = Prb.Axis().YDirection(); Standard_Real S = ( Ox.X() * Oy.Y() - Ox.Y() * Oy.X() > 0.) ? 1 : -1; // poles expressed in the reference mark poles->ChangeArray1()(1) = gp_Pnt2d( ( UF * UF) / ( 2. * p), S * UF ); poles->ChangeArray1()(2) = gp_Pnt2d( ( UF * UL) / ( 2. * p), S * ( UF + UL) / 2. ); poles->ChangeArray1()(3) = gp_Pnt2d( ( UL * UL) / ( 2. * p), S * UL ); // replace the bspline in the mark of the parabola gp_Trsf2d Trsf; Trsf.SetTransformation( Prb.Axis().XAxis(), gp::OX2d()); poles->ChangeArray1()(1).Transform( Trsf); poles->ChangeArray1()(2).Transform( Trsf); poles->ChangeArray1()(3).Transform( Trsf); }
由上面的代码可知,先设置曲线次数为2,再设置节点矢量为[UF,UF,UF,UL,UL,UL],即首参数UF和末参数UL的重数皆为3,由节点矢量可知转换后的NURBS曲线为Bezier曲线。
三个控制顶点对应的权因也都设置为1。三个控制顶点计算方法按上一节中所述。关键是P1点的计算。上面的计算方法仅为个人观点,欢迎讨论交流。
最后根据有理Bezier曲线的仿射不变性:对有理Bezier曲线进行旋转、平移和缩放变换,其表达式不变,只是控制点发生了改变。新的控制点可以通过对原控制点作变换得到。即要对有理Bezier曲线进行仿射变换,只需对其控制点作变换即可。
圆锥截线的转换类的使用是很简单的,且计算都是在构造函数中完成。下面给出一个将抛物线转换为NURBS曲线的具体示例来说明其用法。
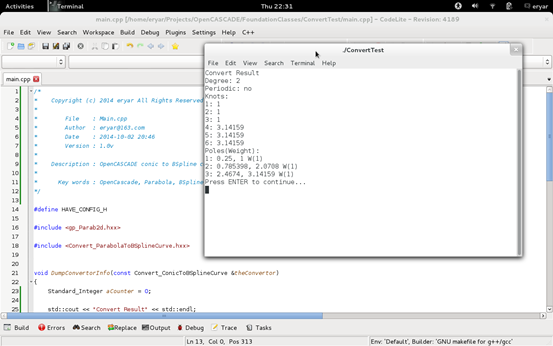
/* * Copyright (c) 2014 eryar All Rights Reserved. * * File : Main.cpp * Author : eryar@163.com * Date : 2014-10-02 20:46 * Version : 1.0v * * Description : OpenCASCADE conic to BSpline curve-Parabola. * * Key words : OpenCascade, Parabola, BSpline Curve, Convert */ #define HAVE_CONFIG_H #include <gp_Parab2d.hxx> #include <Convert_ParabolaToBSplineCurve.hxx> void DumpConvertorInfo(const Convert_ConicToBSplineCurve &theConvertor) { Standard_Integer aCounter = 0; std::cout << \"Convert Result\" << std::endl; std::cout << \"Degree: \" << theConvertor.Degree() << std::endl; std::cout << \"Periodic: \" << (theConvertor.IsPeriodic() ? \"yes\" : \"no\") << std::endl; std::cout << \"Knots: \" << std::endl; for (Standard_Integer i = 1;i <= theConvertor.NbKnots(); ++i) { for (Standard_Integer j = 1; j <= theConvertor.Multiplicity(i); ++j) { std::cout << ++aCounter << \": \" << theConvertor.Knot(i) << std::endl; } } std::cout << \"Poles(Weight): \" << std::endl; for (Standard_Integer i = 1; i <= theConvertor.NbPoles(); ++i) { gp_Pnt2d aPole = theConvertor.Pole(i); std::cout << i << \": \" << aPole.X() << \", \" << aPole.Y() << \" W(\" << theConvertor.Weight(i) << \")\" << std::endl; } } void TestParabolaConversion(void) { gp_Parab2d aParabola(gp::OX2d(), 1.0); Convert_ParabolaToBSplineCurve aConvertor(aParabola, 1.0, M_PI); DumpConvertorInfo(aConvertor); } int main(int argc, char **argv) { TestParabolaConversion(); return 0; }
程序开始部分需要定义HAVE_CONFIG_H,这与在Windows中编程定义WNT有所不同。程序输出结果如下图所示:
Figure 4.1 Convert Parabola to BSpline Curve Result
5. Conclusion
NURBS的一个优势就是统一了曲线曲面的表示方法,即不仅可以表示自由曲线曲面,还可精确表示圆锥曲线曲面。其中抛物线是最简单的圆锥截线,从简单的抛物线转换成NURBS曲线着手,学习NURBS是如何来表示圆锥截线的。
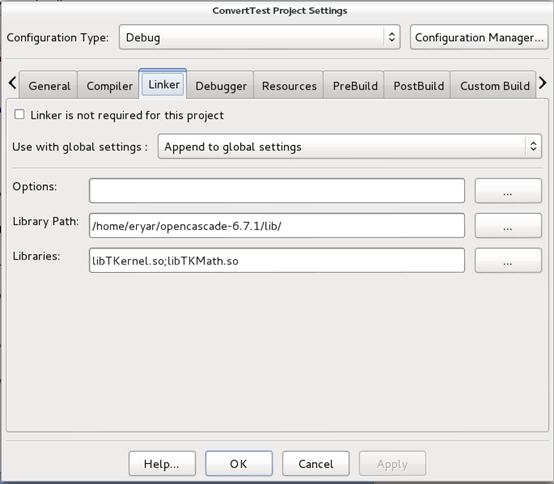
第一次使用Debian系统来编程,选用了一个轻量级的IDE开发工具Codelite,用法与Visual Studio类似。期间也遇到包含引用目录及程序运行时找不到动态库的问题。其中在Codelite中添加引用库路径的方法如下图所示:
Figure 5.1 Set Library Path and Add Libraries in Codelite
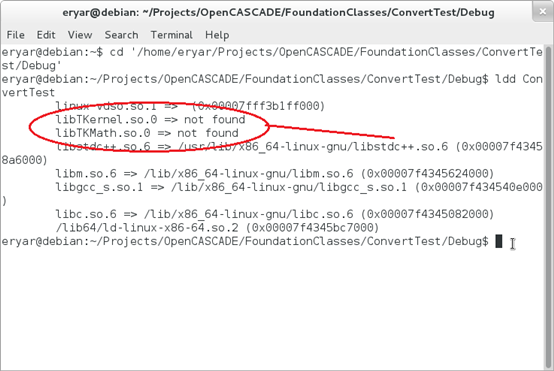
添加上述引用库后,解决了链接错误,但是直接运行程序,发现也有与在Windows中类似的问题,即缺少依赖的动态库,如下图所示为使用lld命令检查程序的依赖项。最后通过向ld.so.conf中添加动态库所在的目录解决了问题。相关命令如下所示:
include ld.so.conf.d/*.conf
# echo \”/home/eryar/opencascade-6.7.1/lib\” >> /etc/ld.so.conf
# ldconfig
注:以上命令需要有root权限。
Figure 5.2 Use lld command to check depends
通过解决以上的问题,来适应在Debian中使用Codelite开发程序。
6. References
1. 人民教育出版社中学数学室. 数学第二册(上). 人民教育出版社. 2000
2. 赵罡,穆国旺,王拉柱译. 非均匀有理B样条. 清华大学出版社. 2010
3. 王仁宏,李崇君,朱春钢. 计算几何教程. 科学出版社. 2008
PDF Version and Sample Code: OpenCASCADE Conic to BSpline Curves-Parabola



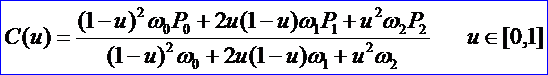
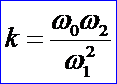

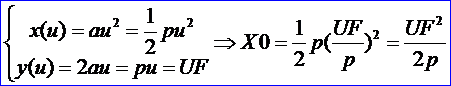

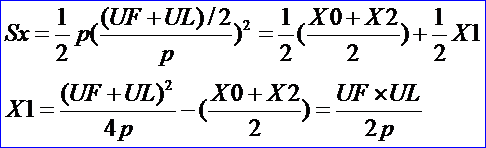
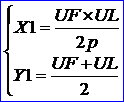

![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)










