OpenCascade Ruled Surface
Abstract. A ruled surface is formed by moving a line connecting points of equal relative arc length or equal relative parametric value on two parametric curves from a start point to a terminate point on the curves. The paper focus on the ruled surface in opencascade.
Key words. OpenCascade, Ruled Surface, 直纹面
1.Introduction
《解析几何》中有关于直纹面Ruled Surface的定义:一曲面S称为直纹面,如果存在一族直线使得这一族中的每一条直线全在S上。并且S上的每个点都在这一族的某一条直线上。这样一族直线称为S的一族直母线。其参数方程为:
即可以将直纹面看作是曲面对当v=0和1时得到的两个边界曲线之间进行线性插值得到的曲面。
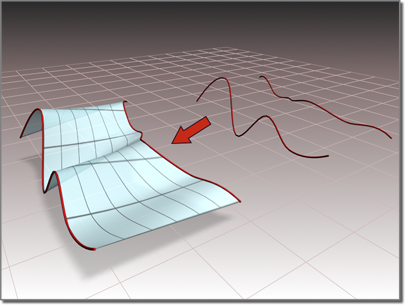
Autodesk 3DS Max中的直纹面,图片来自:
直纹面是从两条曲线来构造曲面的方法,Coons曲面是由四边条界曲线来构造曲面,理解直纹面的构造原理,为进一步理解通用的放样Sweep造型打下基础。
2.Ruled Surface Parametric Equation
直纹面的参数方程也可以写成如下形式:
直接根据参数方程可以定义出相应的直纹面。在OpenCASCADE中话,可以从Geom_Surface派生新的类,并实现相应的虚函数。如实现计算对应参数u,v的值的虚函数D0()等。为了简单起见,用相应的函数计算直纹面上的点,并生成OpenCASCADE Draw Test Harness的命令脚本文件,方便在Draw中可视化。
如有名的Mobius Strip也是个直纹面:
Mobius Strip的参数方程为:
根据上述参数方程在OpenCASCADE的Draw生成Mobius Strip,代码如下所示:
const Standard_Real MOBIUS_RADIUS = 50.0; void MobiusStrip(Standard_Real theU, Standard_Real theV, gp_Pnt& thePoint) { thePoint.SetX((MOBIUS_RADIUS + theU * Cos(0.5 * theV)) * Cos(theV)); thePoint.SetY((MOBIUS_RADIUS + theU * Cos(0.5 * theV)) * Sin(theV)); thePoint.SetZ(theU * Sin(0.5 * theV)); } void TestMobiusStrip() { std::ofstream aTclFile(\"d:/mobius.tcl\"); aTclFile << \"pload ALL\" << std::endl; aTclFile << \"vinit\" << std::endl; Standard_Real aWidth = 10.0; Standard_Integer aN = 0; for (Standard_Real s = -aWidth; s < aWidth; s += 1.0) { aTclFile << \"polyline p\" << ++aN ; for (Standard_Real t = 0.0; t < M_PI * 2.0; t += 0.01) { gp_Pnt aPoint; MobiusStrip(s, t, aPoint); aTclFile << \" \" << aPoint.X() << \" \" << aPoint.Y() << \" \" << aPoint.Z(); } aTclFile << \"\\n vdisplay p\" << aN << std::endl; } for (Standard_Real t = 0.0; t < M_PI * 2.0; t += 0.2) { aTclFile << \"polyline p\" << ++aN; gp_Pnt aPoint; MobiusStrip(-aWidth, t, aPoint); aTclFile << \" \" << aPoint.X() << \" \" << aPoint.Y() << \" \" << aPoint.Z(); MobiusStrip(aWidth, t, aPoint); aTclFile << \" \" << aPoint.X() << \" \" << aPoint.Y() << \" \" << aPoint.Z(); aTclFile << \"\\n vdisplay p\" << aN << std::endl; } } int main(int argc, char* argv[]) { TestMobiusStrip(); return 0; }
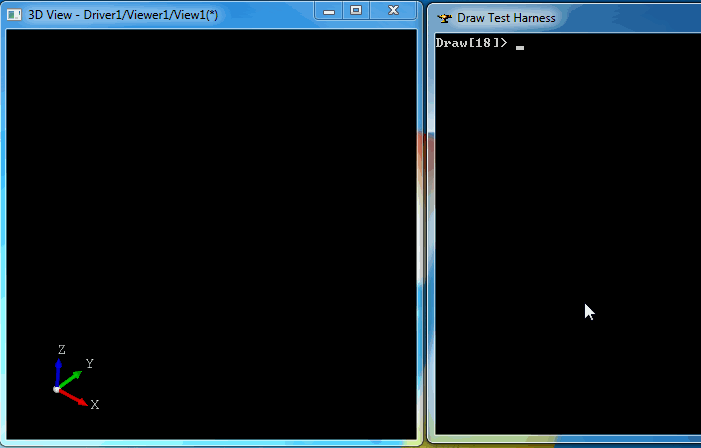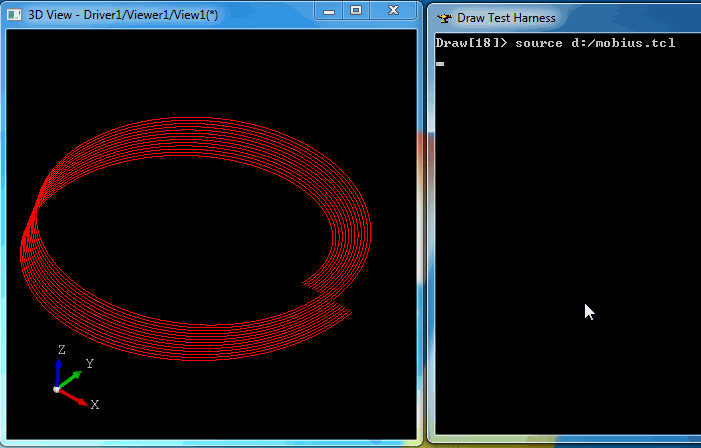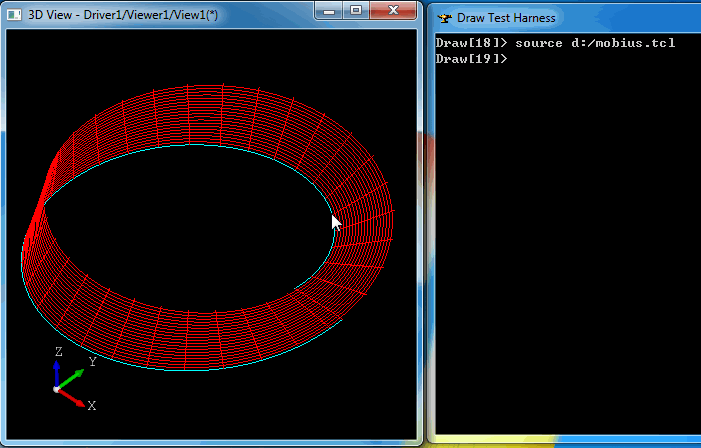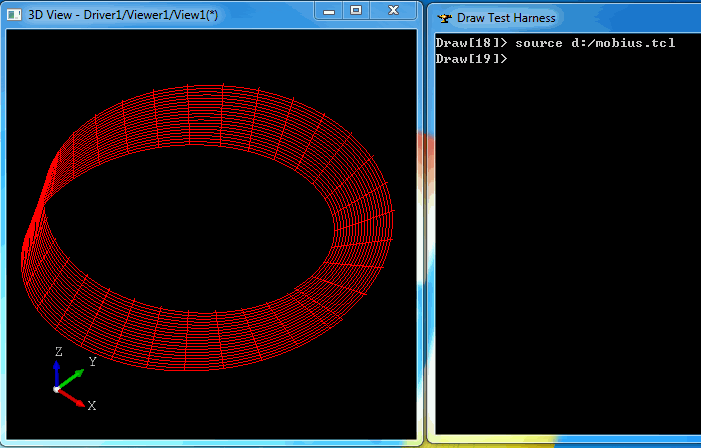
在D盘生成一个mobius.tcl脚本文件,直接在Draw Test Harness中输入命令:
source d:/mobius.tcl
即可得到如下图所示的Mobius环:
其他的直纹面只要知道参数方程,都可以采用这种方法在OpenCASCADE Draw Test Harness中进行显示。有人也用POV-Ray根据直纹面的参数方程来绘制直纹面,效果更不错。
这是使用参数方程来表示直纹面的方法,如果知道直纹面的参数方程,可以从几何曲面来派生新类Geom_Surface,并实现几个相关虚函数,应该可以直接给OpenCASCADE显示了,这种方法没有测试。
3.Ruled Surface to B Spline Surface
如果已知直纹面的参数方程,如何用NURBS曲面来表示直纹面呢?在《非均匀有理B样条》一书中给出了一种将给定两条曲线C1,C2转换成直纹面的方法。他给出的限制条件是想要生成在v方向是直线的曲面,即是C1(u)和C2(u)之间的线性插值。而且还要求在两条曲线的等参数点之间进行插值。又由于曲面是张量各曲面,两条边界曲线C1和C2必须具有相同的次数,并定义在相同的节点矢量上,因此表示这样的直纹面的B样条转换过程为:
l 确保两条曲线定义在相同的参数区间内;
l 确保两条曲线的次数相同。如果不同,则将次数低的曲线升阶;
l 确保两条曲线有相同的节点矢量。
OpenCASCADE中生成直纹面的是类GeomFill的静态函数Surface(),其实现步骤与上述类似,具体实现的类是GeomFill_Profiler。GeomFill_Profiler是个更通用的类,它可以根据多条曲线来构造曲面。下面通过Draw Test Harness脚本来根据两条曲线构造直纹面。
3.1 根据两条直线构造直纹面
# Ruled surface between two lines. vertex v1 0 0 0 vertex v2 0 8 8 vertex v3 8 0 8 vertex v4 8 8 0 edge e1 v1 v2 edge e2 v3 v4 pruled r1 e1 e2 vdisplay v1 v2 v3 v4 e1 e2 r1
生成直纹面是一个双线性曲面,如下图所示:
3.2 根据两个圆构造直纹面
# Ruled surface between circle and ellipse. circle c1 0 0 0 5 circle c2 0 0 10 4 mkedge e3 c1 mkedge e4 c2 pruled r2 e3 e4 vdisplay e3 e4 r2
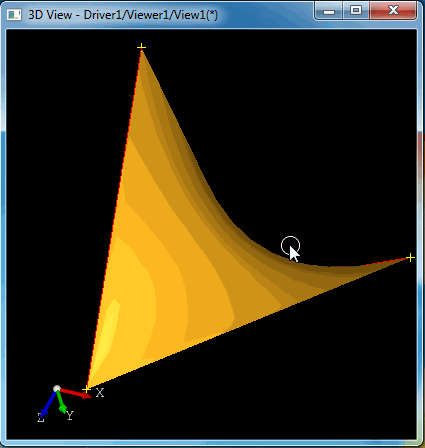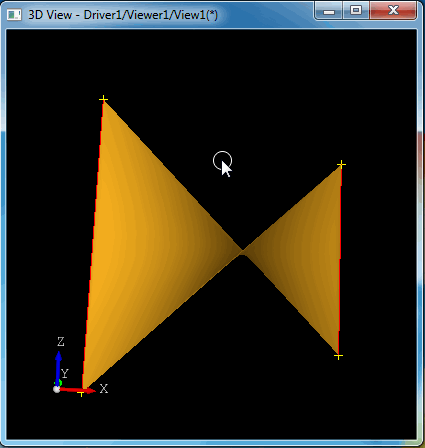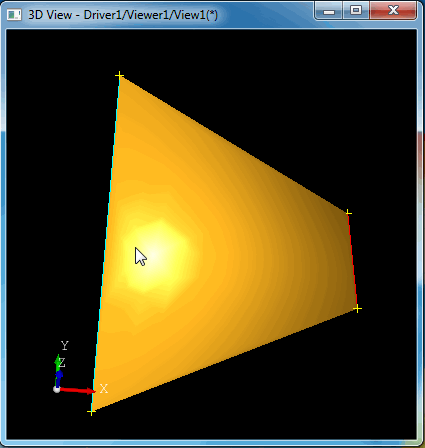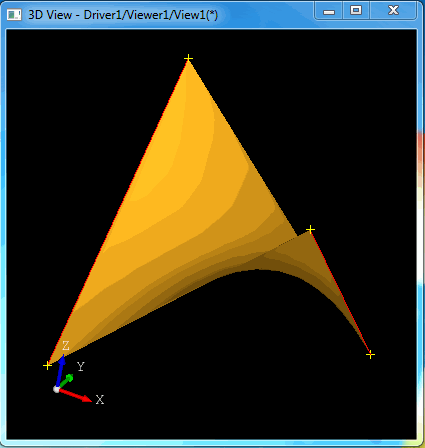
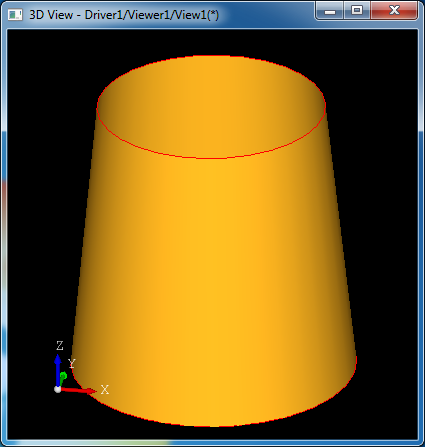
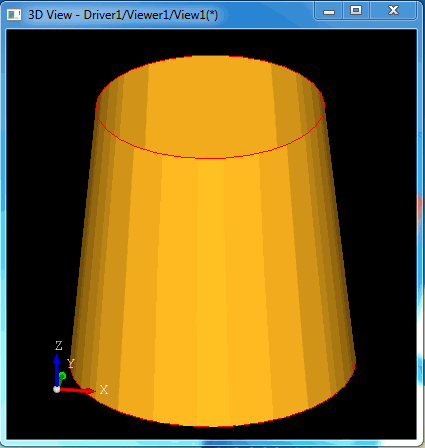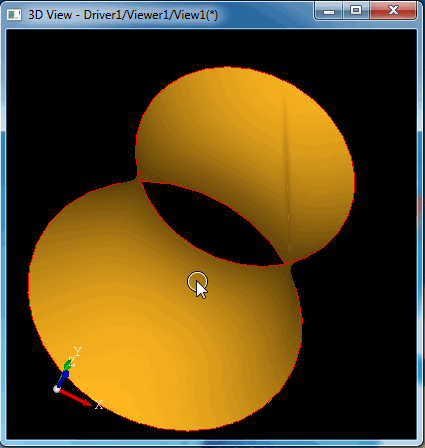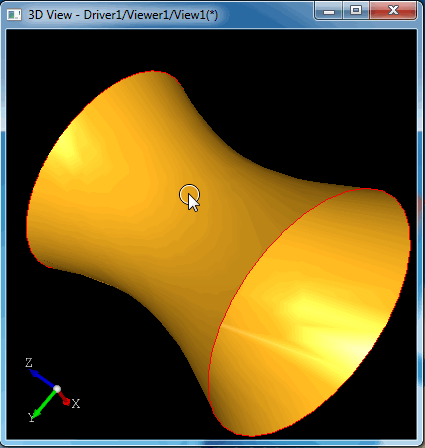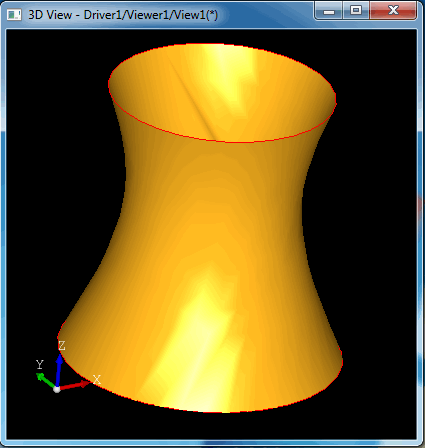
生成的直纹面是一个圆锥面,效果如下图所示:
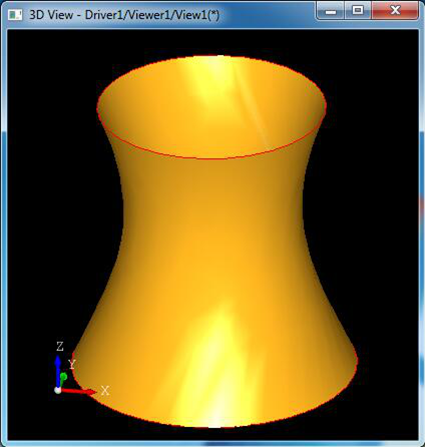
当顶部的圆旋转时会得到如下图所示的直纹面:
相应的Draw脚本如下:
# Ruled surface between circle and ellipse. circle c1 0 0 0 5 circle c2 0 0 10 4 mkedge e3 c1 mkedge e4 c2 pruled r2 e3 e4 vdisplay e3 e4 r2 wait 2 trotate e4 0 0 0 0 0 1 30 pruled r2 e3 e4 vdisplay r2 wait 2 trotate e4 0 0 0 0 0 1 30 pruled r2 e3 e4 vdisplay r2 wait 2 trotate e4 0 0 0 0 0 1 30 pruled r2 e3 e4 vdisplay r2
生成的动画效果如下图所示:
4.Conclusion
根据直纹面的参数方程就可以绘制出相应的曲面,然后如何用B样条曲面来表示直纹面,需要满足一定的条件。IGES中定义的直纹面就给出了两种方式:等弧长和等参数构造。引用《非均匀有理B样条》书中对两种形式的说明如下:一般情况下,连接两条曲线上相对弧长相等的点会产生一个几何上不同的曲面,而这样的曲面不能通过NURBS来表示。因此,要在NURBS的直纹面和IGES的直纹面(Type 118 Form 0/1)之间进行数学上的精确转换是不可能的。
OpenCASCADE的直纹面也是使用的NURBS表示,所以其也是等参数形式的直纹面。希望在理解根据两条曲线来构造曲面的方法来理解更一般的造型算法,即通过多条曲线来构造曲面的造型方法。
5.References
1. Weisstein Eric W. “Ruled Surface”. http://mathworld.wolfram.com/RuledSurface.html
2. www.ms.uky.edu/~lee/visual05/gallery/ruledsurfaces.doc
3. The Initial Graphics Exchange Specification (IGES) Version 6.0
4. 赵罡, 穆国旺, 王拉柱. 非均匀有理B样条. 清华大学出版社. 2010
5. 丘维声. 解析几何. 北京大学出版社. 1996
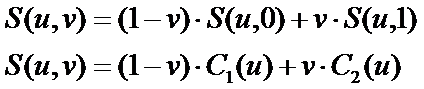


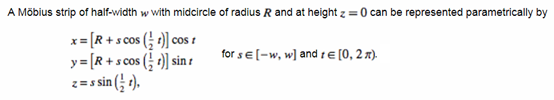








暂无评论内容