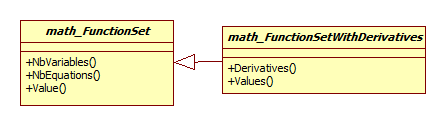
Function Set in OPEN CASCADE
Abstract. The common math algorithms library provides a C++ implementation of the most frequently used mathematical algorithms. These include: algorithms to solve a set of linear algebraic equations, algorithms to find the minimum of a function of one or more independent variables, algorithms to find roots of one, or of a set of non-linear equations, algorithm to find the eigenvalues and eigenvectors of a square matrix. The solver for function set is used widely in extrema value evaluation, point project on to curve and surface, also used to solve the point inverse for geometry curve and surface. The paper focus on the function set concept and its solver in OPEN CASCADE.
Key Words. Function Set, Non-Linear Equation Solver, Equations Root,
1. Introduction
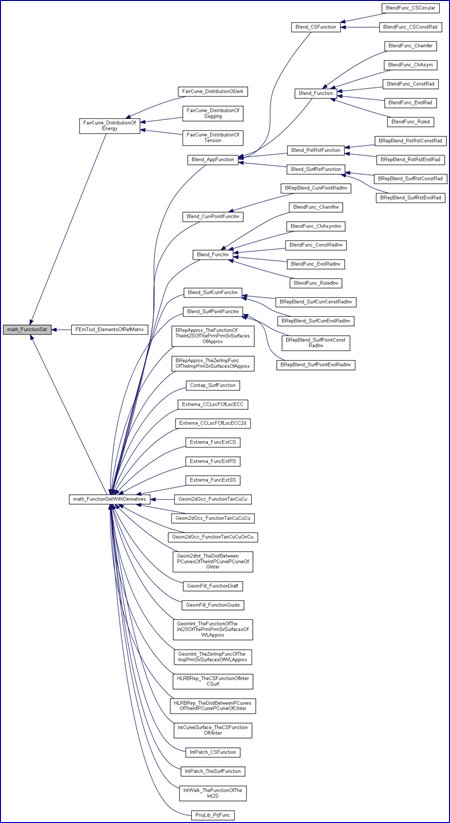
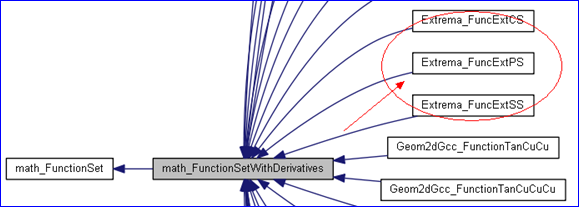
OPEN CASCADE的math包中提供了常见的数值计算的功能,如矩阵的加减乘除,转置及方阵的特征值和特征向量的计算,求解线性方程组;一元函数或多元函数的微分、积分及极值的计算;线性和非线性(Non-Linear Equations)方程组(Function Set)的计算等等。大部分功能和另一个开源科学计算库gsl类似,只是采用面向对象的方式,更便于使用。方程组(Function Set)的相关计算与多元函数(MultiVarFunction)一样地在OPEN CASCADE库广泛地应用,如一些极值计算算法,拟合算法、点在曲线曲面上投影的相关问题等等,都会涉及到方程组求解的计算。如下类图所示。
下面的类图为方程组类Math_FunctionSet的类图,由类图可知,从其派生的类数量很多,由此可见其在OPEN CASCADE中的重要性。本文主要对其用法进行说明,理解其用法后,便于对其他相关算法的理解。
在理解math包中大部分算法后,也是掌握了一个数学计算工具,以后遇到相关的问题,可以尽量地用数学的方式进行解决,提高数学的应用水平。
Figure 1.1 math_FunctionSet class diagram in OPENCASCADE
2. Function Set
很多科学理论和工程技术问题都最终转化成非线性方程或方程组的求解,如对理论数据或实验观察的数据进行拟合用到的最小二乘法,就是一个典型的非线性方程组求解的问题。而在几何中的应用就更广泛了,像计算直线与平面的交点问题,点到自由曲线曲面的投影问题等等。鉴于方程组的广泛应用,OPEN CASCADE的数学包中提供了一个抽象类math_FunctionSet来与之对应,方便方程组在程序中的计算。
对于普通的方程组,主要设置了三个抽象函数:
v NbVariables():方程组中变量的个数;
v NbEquations():方程组中方程的个数;
v Value():计算指定变量的方程组的值;
带微分的方程组类比普通方程组多两个抽象函数:
v Derivatives():计算指定变量的方程组的微分值;
v Values():计算指定变量的方程组的值和微分值;
因为都是抽象类,所以不能直接使用。下面结合《计算方法》书中的题目,来说明方程组在OPENCASCADE中的计算方法。下面的题目来自《计算方法》第二版P213页例17:设有非线性方程组:
从几何上看其解就是圆和曲线的交点。下面给出OPENCASCADE中的计算代码:
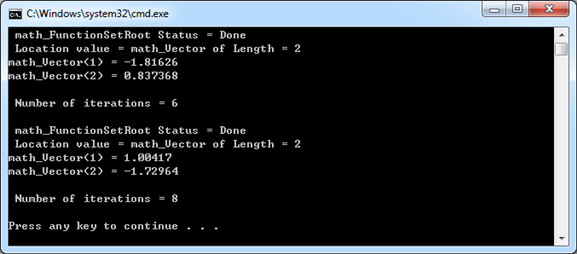
/* * Copyright (c) 2016 Shing Liu All Rights Reserved. * * File : main.cpp * Author : Shing Liu(eryar@163.com) * Date : 2016-01-12 21:00 * Version : OpenCASCADE6.9.0 * * Description : test function set. */ #define WNT #include <math_FunctionSetRoot.hxx> #include <math_FunctionSetWithDerivatives.hxx> #pragma comment(lib, \"TKernel.lib\") #pragma comment(lib, \"TKMath.lib\") /** * @brief test function for a circle and a curve: * * F1(x1,x2) = (x1)^2 + (x2)^2 -4 * F2(x1,x2) = e^(x1) + x2 - 1 * * The derivatives of the function set are: * Dx1f1(x1,x2) = 2.0 * x1 * Dx2f1(x1,x2) = 2.0 * x2 * Dx1f2(x1,x2) = e^(x1) * Dx2f2(x1,x2) = 1.0 */ class test_FunctionSet: public math_FunctionSetWithDerivatives { public: virtual Standard_Integer NbVariables() const { return 2; } virtual Standard_Integer NbEquations() const { return 2; } virtual Standard_Boolean Value(const math_Vector& X, math_Vector& F) { F(1) = X(1) * X(1) + X(2) * X(2) - 4.0; F(2) = exp(X(1)) + X(2) - 1.0; return Standard_True; } virtual Standard_Boolean Derivatives(const math_Vector& X, math_Matrix& D) { D(1,1) = 2.0 * X(1); D(1,2) = 2.0 * X(2); D(2,1) = exp(X(1)); D(2,2) = 1.0; return Standard_True; } virtual Standard_Boolean Values(const math_Vector& X, math_Vector& F, math_Matrix& D) { Value(X, F); Derivatives(X, D); return Standard_True; } }; void testFunctionSet(void) { test_FunctionSet aTestFunctionSet; math_FunctionSetRoot aSolver(aTestFunctionSet); math_Vector aStartPoint(1, 2, 0.0); // initial guess point(-2.0, 0.0) aStartPoint(1) = -2.0; aStartPoint(2) = 0.0; aSolver.Perform(aTestFunctionSet, aStartPoint); std::cout << aSolver << std::endl; // initial guess point(0.0, -2.0) aStartPoint(1) = 0.0; aStartPoint(2) = -2.0; aSolver.Perform(aTestFunctionSet, aStartPoint); std::cout << aSolver << std::endl; } int main(int argc, char* argv[]) { testFunctionSet(); return 0; }
计算结果如下图所示:
Figure 2.1 Evaluate result
3. Application
在曲线和曲面的极值计算、曲面和曲面的极值计算及点和曲面的极值计算中都用到了求解方程组的算法,如下类图所示:
Figure 3.1 Extrema algorithms implemented by Function Set
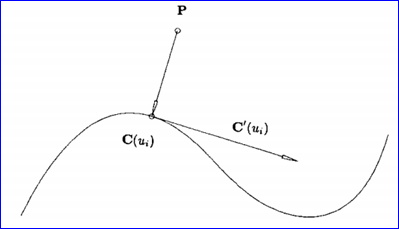
其中点和曲面极值的计算也适用于曲面上点的参数的反求。与曲线上点的参数反求类似,曲线上点的参数反求是计算非线性方程的根;曲面上点的参数反求则扩展到了非线性方程组。问题求解的关键还是建立数学模型,如点到曲线上的投影由下图可知:
Figure 3.2 Point project on curve
构造的函数为:
上式表示曲线上过参数u的切线与曲线上参数u的点到指定点的向量的数量积,当f(u)=0时数量积为0,即为点垂直于曲线上过参数u的切线,对此非线性方程求解,即得到了点到曲线的投影。同理,点到曲面的投影也可以建立类似的方程组:
其中曲面对参数u,v的偏导数表示在曲面在u,v方向上的切线,两个函数意义和一个方程的意义类似,即点到曲面上某一点的向量与切线的数量积。当向量与两个切线方向的数量积为0的时候,即此向量与这两个切线都垂直,就是点到曲面的投影。这也是OPEN CASCADE中计算点与曲面极值的实现原是,其类为Extrema_FuncExtPS,为了使用类math_FunctionSetRoot对方程组进行求解,Extrema_FuncExtPS也是由类math_FunctionSetWithDerivatives派生,类定义代码如下:
//! Functional for search of extremum of the distance between point P and //! surface S, starting from approximate solution (u0, v0). //! //! The class inherits math_FunctionSetWithDerivatives and thus is intended //! for use in math_FunctionSetRoot algorithm . //! //! Denoting derivatives of the surface S(u,v) by u and v, respectively, as //! Su and Sv, the two functions to be nullified are: //! //! F1(u,v) = (S - P) * Su //! F2(u,v) = (S - P) * Sv //! //! The derivatives of the functional are: //! //! Duf1(u,v) = Su^2 + (S-P) * Suu; //! Dvf1(u,v) = Su * Sv + (S-P) * Suv //! Duf2(u,v) = Sv * Su + (S-P) * Suv = Dvf1 //! Dvf2(u,v) = Sv^2 + (S-P) * Svv //! //! Here * denotes scalar product, and ^2 is square power. class Extrema_FuncExtPS : public math_FunctionSetWithDerivatives { public: DEFINE_STANDARD_ALLOC Standard_EXPORT Extrema_FuncExtPS(); Standard_EXPORT Extrema_FuncExtPS(const gp_Pnt& P, const Adaptor3d_Surface& S); //! sets the field mysurf of the function. Standard_EXPORT void Initialize (const Adaptor3d_Surface& S); //! sets the field mysurf of the function. Standard_EXPORT void SetPoint (const gp_Pnt& P); Standard_EXPORT Standard_Integer NbVariables() const Standard_OVERRIDE; Standard_EXPORT Standard_Integer NbEquations() const Standard_OVERRIDE; //! Calculate Fi(U,V). Standard_EXPORT Standard_Boolean Value (const math_Vector& UV, math_Vector& F) Standard_OVERRIDE; //! Calculate Fi\'(U,V). Standard_EXPORT Standard_Boolean Derivatives (const math_Vector& UV, math_Matrix& DF) Standard_OVERRIDE; //! Calculate Fi(U,V) and Fi\'(U,V). Standard_EXPORT Standard_Boolean Values (const math_Vector& UV, math_Vector& F, math_Matrix& DF) Standard_OVERRIDE; //! Save the found extremum. Standard_EXPORT virtual Standard_Integer GetStateNumber() Standard_OVERRIDE; //! Return the number of found extrema. Standard_EXPORT Standard_Integer NbExt() const; //! Return the value of the Nth distance. Standard_EXPORT Standard_Real SquareDistance (const Standard_Integer N) const; //! Returns the Nth extremum. Standard_EXPORT const Extrema_POnSurf& Point (const Standard_Integer N) const; protected: private: gp_Pnt myP; Adaptor3d_SurfacePtr myS; Standard_Real myU; Standard_Real myV; gp_Pnt myPs; TColStd_SequenceOfReal mySqDist; Extrema_SequenceOfPOnSurf myPoint; Standard_Boolean myPinit; Standard_Boolean mySinit; };
根据其注释可知,建立的方程组和上述方程组相同,并且还计算了方程组的一阶偏导数如下:
通过类math_FunctionSetRoot对上述方程组进行求解,即可得到点到曲面的极值。
4. Conclusion
线性和非线性方程组的求解在几何中也有大量的应用。线性方程组可以利用矩阵的概念进行求解,如Gauss消元法。而非线性方程组的求解也是有相关的算法,如Newton法等,具体理论可参考《计算方法》等相关书籍。掌握这些数学工具之后,关键是将几何问题抽象成数学问题,然后利用这些数学工具来解决实际问题。从而可以将《高等数学》、《线性代数》等理论知识,通过《计算方法》在计算机中的实现,来用理论指导实践,通过实践加深理论的理解。也让枯燥的理论更生动、有趣。
与OPEN CASCADE数学包中其他概念如一元函数,多元函数等概念一样,非线性方程组及其求解也是一个重要概念。理解这些类的原理之后,便于对其他几何造型算法的实现原理进行理解。
5. References
1. 赵罡, 穆国旺, 王拉柱译. 非均匀有理B样条. 清华大学出版社. 1995
2. 易大义, 陈道琦. 数值分析引论. 浙江大学出版社. 1998
3. 易大义,沈云宝,李有法. 计算方法. 浙江大学出版社. 2002
4. 蒋尔雄,赵风光,苏仰锋. 数值逼近. 复旦大学出版社. 2012
5. 王仁宏,李崇君,朱春钢. 计算几何教程. 科学出版社. 2008
6. 同济大学数学教研室. 高等数学. 高等教育出版社. 1996
7. 同济大学应用数学系. 线性代数. 高等教育出版社. 2003
PDF Version: Function Set in OPEN CASCADE

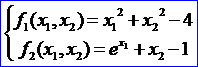
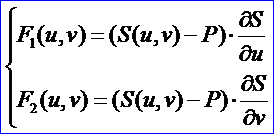
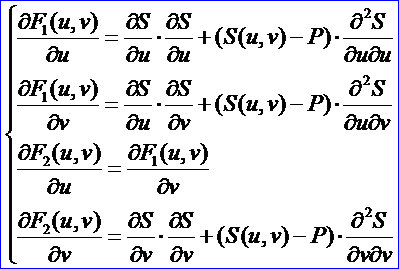








暂无评论内容