原理
算法伪代码如下:
remesh(target_edge_length)
low = 4/5 * target_edge_length
high = 4/3 * target_edge_length
for i = 0 to 10 do
spilt_long_edges(high)
collapse_short_edges(low, high)
equalize_valences()
tangential_relaxation()
project_to_surface()
其中target_edge_length是网格的目标长度。
涉及的三个操作如下:
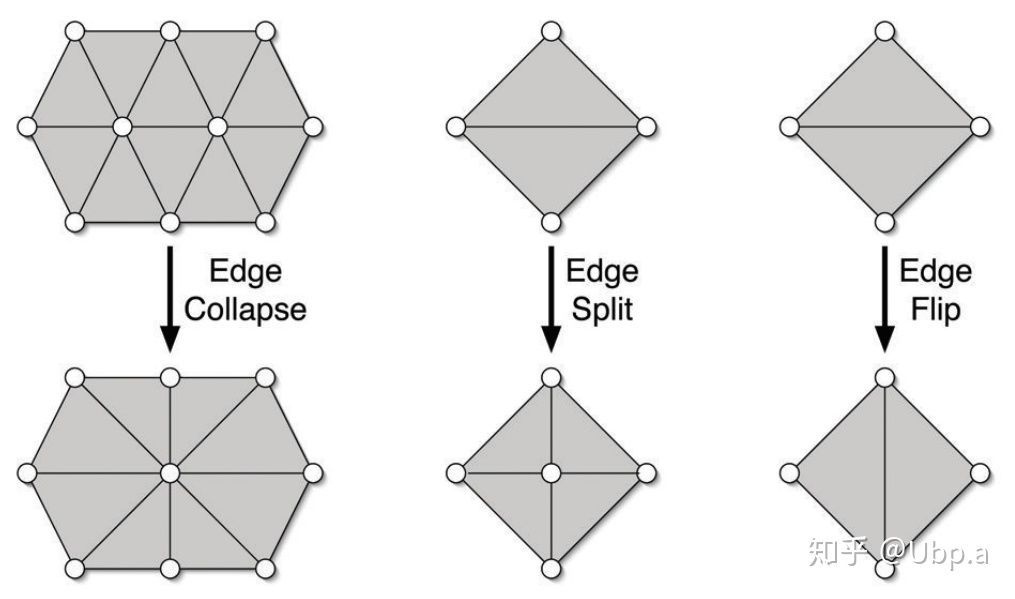
spilt_long_edges
该步骤将所有长于high = 4/3 * target_edge_length的边进行 Edge Spilt 操作。
collapse_short_edges
该步骤将所有短于low = 4/5 * target_edge_length的边进行 Edge Collapse 操作,新增的点位置为边两端点的中点,另外要求新的边不会长于high = 4/3 * target_edge_length。
equalize_valences
该步骤目的是平衡顶点的度数,最佳度数 optimal valence 为
- 内部点:6
- 边界点:4
通过使用Edge Flip进行顶点度数的增加和减少。

tangential_relaxation和project_to_surface
该步骤解决三角形面积问题,实现网格面积的均匀化。

以上内容转自:Isotropic Remeshing – 知乎 (zhihu.com)
CGAL代码实现
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/remesh.h>
#include <CGAL/Polygon_mesh_processing/border.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <boost/iterator/function_output_iterator.hpp>
#include <CGAL/draw_surface_mesh.h>
#include <iostream>
#include <string>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Surface_mesh<K::Point_3> Mesh;
typedef boost::graph_traits<Mesh>::halfedge_descriptor halfedge_descriptor;
typedef boost::graph_traits<Mesh>::edge_descriptor edge_descriptor;
namespace PMP = CGAL::Polygon_mesh_processing;
struct halfedge2edge
{
halfedge2edge(const Mesh& m, std::vector<edge_descriptor>& edges)
: m_mesh(m), m_edges(edges)
{}
void operator()(const halfedge_descriptor& h) const
{
m_edges.push_back(edge(h, m_mesh));
}
const Mesh& m_mesh;
std::vector<edge_descriptor>& m_edges;
};
int main(int argc, char* argv[])
{
const std::string filename = "data/simple80_complete.stl";
Mesh mesh;
if (!PMP::IO::read_polygon_mesh(filename, mesh) || !CGAL::is_triangle_mesh(mesh))
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
CGAL::draw(mesh, "source mesh");
double target_edge_length = 1;
unsigned int nb_iter = 5;
std::cout << "Split border...";
std::vector<edge_descriptor> border;
PMP::border_halfedges(faces(mesh), mesh, boost::make_function_output_iterator(halfedge2edge(mesh, border)));
PMP::split_long_edges(border, target_edge_length, mesh);
std::cout << "done." << std::endl;
std::cout << "Start remeshing of " << filename
<< " (" << num_faces(mesh) << " faces)..." << std::endl;
PMP::isotropic_remeshing(faces(mesh), target_edge_length, mesh,
CGAL::parameters::number_of_iterations(nb_iter)
.protect_constraints(true)); //i.e. protect border, here
std::cout << "Remeshing done." << std::endl;
CGAL::draw(mesh, "remeshing mesh");
return 0;
}




关键函数
template<typename PolygonMesh , typename FaceRange , typename NamedParameters = parameters::Default_named_parameters>
void CGAL::Polygon_mesh_processing::isotropic_remeshing (const FaceRange & faces,
const double & target_edge_length,
PolygonMesh & pmesh,
const NamedParameters & np = parameters::default_values()
)
| 参数名 | 解释 |
|---|---|
| pmesh | a polygon mesh with triangulated surface patches to be remeshed |
| faces | the range of triangular faces defining one or several surface patches to be remeshed |
| target_edge_length | the edge length that is targeted in the remeshed patch. If 0 is passed then only the edge-flip, tangential relaxation, and projection steps will be done. |
| np | an optional sequence of Named Parameters among the ones listed below |
pmesh:可以是
Surface_mesh或者Polyhedron_3。faces:可以通过
faces(mesh)返回boost::graph_traits<CGAL::Surface_mesh<P>>::face_iterator的序列。其中CGAL::Surface_mesh<P>为PolygonMesh。target_edge_length:同上述原理。
对于np参数,如下列出几个常用的
-
number_of_iterations:执行edge splits, edge collapses, edge flips, tangential relaxation and projection to the initial surface的迭代次数。默认值为1。 -
edge_is_constrained_map:包含pmesh的每个边的受约束或不受约束状态的属性映射。默认没有边被约束。 -
protect_constraints:如果为true,在edge_is_constrained_map(或者默认边界) 中的边在重建过程中不进行split和collapsed操作。默认为false。注意:如果
protect_constraints为true的话,受约束的边不能大于4/3*target_edge_length。因此需要在这执行isotropic_remeshing()之前先执行split_long_edges()进行长边分割。 -
do_split、do_collapse、do_flip、do_project都是布尔类型值。默认都为true。
问题与总结
在测试中,两个模型都是封闭的流形表面,故不存在边界。因此,无论protect_constraints取何值,remeshing后原模型面与面的过渡直线上的边将会变化,致使结果模型的棱边凹凸不平。为了验证上述猜想,使用带边界的三角网格进行如下测试:



可以看到,当将protect_constraints置为true时(第三张图),边界上的边受到了约束,因此remeshing后不如protect_constraints置为false(第二张图)时的均匀。
因此,为了实现闭合网格remeshing前后棱边形状不变,我们可以将棱边上的边属性映射为受约束,而其余边属于映射为不受约束,得到表面网格的edge_is_constrained_map,再置protect_constraints为true,实现对这些边的保护。










![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)







