1、前言

记得大约是在10多年前，还在我努力的在学习着DirectX编程和3D引擎编程的方方面面知识的时候，初次接触到了当时很先进的Shader程序。当时搜集了很多资料，其中有一份就是讲解如何在PixelShader中实现类似PhotoShop中的一些滤镜功能。

这次我就将这些陈年的有意思的Shader翻出来，用D3D12再次回炉一下，也做成教程，供大家学习Shader使用。

本章的源代码已经全部上传到GitHub上，大家可以下载参考学习。

从本章开始，教程的重心将转移到Shader（HLSL）的编写等方面上来，因为我们已经学习了包括实时光追渲染（DXR）的基本编程方法在内的很多C++侧编程调用D3D12接口的技能了，整个教程作为D3D12接口的基本使用方法来说，这部分学习基本可以暂告一个段落了。接着我们就进入Shader编程的部分，因为Shader才是驱动GPU实现“光影魔法”的真正技能！（注：可能重点将放在Raytracing Shader方面，因为DXR自带例子中这部分的Shader实在是太恶心了，而且被搞成了光栅化渲染Shader的附庸，这完全是本末倒置，大家根本体会不到Raytracing Shader的真正魅力。）

本章源码基于之前的多线程渲染的示例，原始运行效果如下：

 

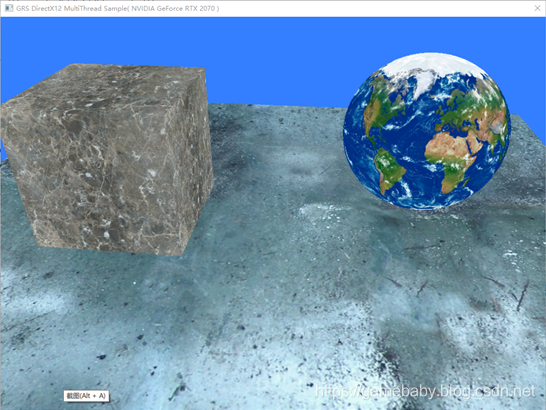
注意图中为了较好的显示本章Pixel Shader滤镜效果，所以球体的纹理换成了地球的纹理，这样在视觉效果上更明显一些。

以后传统光栅化的示例代码，都将使用多线程渲染的示例来作为基础框架，这样做主要的目的：一是为了督促各位认真学习系列教程打牢基础；二是为了让大家牢固掌握并且习惯多线程的基本编程方法；三是让大家在习惯多线程渲染的基础上能够产生一些有“灵感”的想法，尽快从基础学习的“必然王国”跨越到可以随心所欲发挥创造力的“自由王国”。未来一定是多线程渲染的天下！

2、Shader中的Static变量

为了实现本次教程中的Pixel Shader特效，在Shader中加入了很多参变量，

在此提醒大家：凡是在Shader中（不论什么Shader）的全局变量，全是渲染管线的参数，都需要在C++代码侧的根签名中加以描述，当然唯一的例外就是用static类型修饰符定义的变量。

当Shader中的变量被声明为static型时，那么该变量就仅用于Shader代码内部，也不用声明在根签名中，这样就不必再从C++代码中经过复杂的过程传入Shader中。

在本章示例Shader中，主要是声明了一个指定马赛克效果像素半径范围的变量。当然这个变量也可以不声明为static型，这样就需要定义对应的根签名中的参数，然后从C++代码中传入。如果再为这个变量加上输入控制，那么就可以看到马赛克效果中马赛克大小的变化。各位可以作为练习自行修改一下试试。

这几个变量的声明如下：

static float2 g_v2MosaicSize1 = float2(32.0f, 32.0f);
static float2 g_v2MosaicSize2 = float2(16.0f, 16.0f);

3、通过主线程上传噪声纹理

之前的多线程渲染示例中，主线程其实并没有做什么资源加载复制等等的工作，当然这是例子中将不同的物体放到不同的线程中渲染必然的一个设计实现要求，因为相关的一些数据还是掌握在各自线程手中比较好。

其中有一个没有交代的细节就是关于MVP矩阵的那个全局const buffer，是每个线程都单独创建了一份，并且每次都通过同一个根签名的参数通道上传到渲染管线（GPU），这样每个物体不同的MVP就被不同的对应线程以同样的方式进行处理，这是一个重要的技巧。

然鹅，有一些资源是场景共用的，分配到子线程去渲染处理显然不太合适，因为每个子线程都可能需要使用这类资源，这样就会多出一些额外跨线程共享资源的操作，使问题变得复杂，幸运的是，我们还有主线程可以用来干这些全场景的活计，在本例中，因为效果需要我们要加载一个噪声纹理，而这个噪声纹理就是每个物体渲染都需要的，所以我们就是用主线程来加载它。主线程中有很多命令列表可以使用，示例中我们就使用pICmdListPre命令列表来加载噪声纹理，具体代码就不粘贴了，大家去GitHub上查看即可。这样实际最终的效果就是几个子线程+主线程完成了纹理加载的第一个Copy动作，然后GPU上的复制引擎则完成了第二个Copy动作。

如果想做进一步优化，就可以为每个线程创建独立的Copy命令队列（GPU上往往有多个Copy引擎），然后创建专门的Copy命令列表来执行资源上传的第二个Copy动作。当然这里的优化建议没有提及因为多个线程其实还是需要从硬盘读取初始的资源数据，而这时就不得不跟低速的IO操作打交道了，如果你看过我之前写的一些关于IOCP的文章，那么就可以考虑将渲染子线程改造成可以支持IOCP回调的形式，也就是线程池形式，从而从头到尾最高效的利用所有的系统硬件完成资源上传GPU的动作，也就是加速场景加载的过程。

Ok，这个话题就扯到这里吧，资料我的博客里都有了，剩下的就是各位自己动手丰衣足食了！

4、黑白效果

本次，我们需要实现的第一个PS特效就是图像黑白化。原理就是像素RGB颜色的亮度和各个颜色分量之间的关系的公式：

GrayValue = 0.3 * R + 0.59 * G  + 0.11 * B

根据这个公式，我们将RGB颜色直接转换为其亮度值，并将亮度值重新设置到每个颜色分量，就变成了该像素的灰度颜色，最终整个纹理中的像素都经过这个变换就变成了一张黑白照片：

 

对应的PS代码很简单，如下：

float4 BlackAndWhitePhoto(float4 inColor)
{
    float BWColor = 0.3f * inColor.x + 0.59f * inColor.y + 0.11f * inColor.z;
    return float4(BWColor, BWColor, BWColor, 1.0f);
}

在最终的PSMain函数中，我们如下调用这个效果函数即可：

float4 PSMain(PSInput input) : SV_TARGET
{
    float4 c4PixelColor;
    ……
    else if( 1 == g_nFun )
    {//黑白效果
        c4PixelColor = g_texture.Sample(g_sampler, input.m_v2UV);
        c4PixelColor = BlackAndWhitePhoto(c4PixelColor);
    }
    ……
    return c4PixelColor;
}

代码中，只是简单的取得像素点对应纹理的颜色值，然后利用我们的黑白特效函数计算成黑白颜色值之后返回即可。

其实最终无论PSMain函数中计算过程如何复杂，结果只是为了返回屏幕上一个像素点的颜色而已，是为“着色”，这也是Shader程序被称为“着色器”的缘由。

这里需要注意的就是，为了演示不同的效果，专门设计了一个全局变量来进行控制，因此最终PSMain函数中就会出现一个巨大的if……else if……else……的判断语句，其实这在CPU的代码上不会带来什么大问题，但是对于GPU来说，因为它在条件分支语句硬件支持上的限制，所以这样的结构对于GPU来说是非常影响效率的。在正式的Shader程序中应当避免。因为我比较懒，不想创建那么多PSO或者使用啰嗦的dynamic linker技术，所以就这样写咯，各位看官一定要注意，这个if……else……不在学习范围内。

那么实际的Shader中，可以使用Shader的运行时linker技术（DX中叫做HLSL的动态链接技术，自DX11引入），或切换不同Shader渲染管线的方式来避免这种情况。

另外在我们的例子中，大家要注意一个“后处理”问题，那就是我们可以看到实际的渲染结果更像是对单独某个物体的纹理做了滤镜效果，而不是整个渲染画面，至少天空的背景色还是保留的。大家可以想象一下其实这类滤镜也可以运用到最终整个渲染结果画面上，这种情况通常被称为“后处理”（Post Shader），大家可以思考下怎么修改可以实现这个后处理？这个问题就留给大家自己动手了，有疑问的可以随时留言垂询。

5、浮雕效果

"浮雕"图像效果是指图像的前景前向“凸出”背景。常见于一些纪念碑的雕刻上，要实现浮雕其实非常简单。把图像的一个象素和其左上方的象素进行求差运算，并加上一个灰度。这个灰度就是表示背景颜色。这里设置这个插值为128 (图像RGB的值是0-255)。同时还应该把这两个颜色的差值转换为亮度信息（类似黑白效果中的处理），否则浮雕图像会出现错误的彩色颜色。

在使用HLSL处理浮雕效果的时候，有两个问题我们需要注意一下。

因为在Pixel Shader中纹理的采样坐标[u,v]是归一化的[0-1.0]^2（向量空间表示法），在计算临近像素坐标时，首先需要知道该采样坐标对应的像素坐标，此时需要知道纹理的像素尺寸大小，假设纹理的像素尺寸大小为[w,h]，那么采样点的像素坐标即为[u*w,v*h];计算过程如下图所示：

其次其左上角像素点的像素坐标即为[u*w-1,v*h-1],然后再将这一坐标归一化到[0-1.0]^2之间，即[(u*w-1)/w,(v*h-1)/h],化简后得到[u-1/w,v-1/h];

此时若采样点是左上角或左上两边时，即点[0.0,0.0]、[u,0.0] 或[0.0,v]，其中u>0.0、v>0.0,那么该采样点左上角或左上边的象素的纹理坐标就是[0.0 – 1.0/w,0.0 – 1.0/h]、[u – 1.0/w,0.0 – 1.0/h] 或[0.0 – 1.0/w,v – 1.0/h]，其中至少有一个采样点归一化坐标为负数。

这样我们就面临两个问题：

其一就是Shader中无法知道这个纹理的像素大小。这需要我们在C++代码侧，通过根签名常量参数的形式当作一个const常量设置给HLSL就可以了。或者固定一个纹理的大小比如1024 x 1024，这样也可以。

其二是图像边界处采样点坐标至少有一个是负数，与在[0-1.0]^2区间内的要求相左。这个时候就需要做特殊处理，通常把边界位置的浮雕结果设置成背景颜色。这通常不需要在Shader中去对图像的边界做特殊处理，而只需要将采样器设置为某种连续模式就可以了。在本章例子中为了照顾大多数特效我们设置为WRAP（包裹）模式。

为了传递特效需要的额外参数，我们特意在代码中又定义了一个常量缓冲如下，代码列在下面。

Shader中：

cbuffer PerObjBuffer : register(b1)
{
    uint g_nFun;
    float2 g_v2TexSize;
    float g_fQuatLevel = 2.0f;    //量化bit数，取值2-6
    float g_fWaterPower = 40.0f;  //表示水彩扩展力度，单位为像素
};

C++代码中：

struct ST_GRS_PEROBJECT_CB
{
    UINT    m_nFun;
    XMFLOAT2 m_v2TexSize;
    float   m_fQuatLevel;    //量化bit数，取值2-6
    float   m_fWaterPower;  //表示水彩扩展力度，单位为像素
};

其中g_v2TexSize就是纹理的像素尺寸大小。

根据纹理像素尺寸计算采样点像素坐标，然后再计算临近像素坐标的方法，是一个非常重要的技巧，几乎很多高级的纹理操作中都需要传入纹理尺寸，然后通过将在Shader中归一化的纹理坐标乘以对应纹理像素大小后，可以得到像素坐标，方便计算临近像素的坐标。通常在Shader代码中使用[1.0/w,1.0/h]作为一个像素的归一化坐标偏移量，前面已经有详细推导过程了，建议最好是记住。有了像素便宜量，就可以取得某一像素采样点临近像素（“九宫格”）的颜色值，进行一些混色操作，我们后续的很多特效都使用了这一技巧。

有了上面的基础，我们就可以实现浮雕效果Shader函数如下：

float4 Anaglyph(PSInput input)
{
    //实现浮雕效果
    float2 upLeftUV = float2(input.m_v2UV.x - 1.0 / g_v2TexSize.x
        , input.m_v2UV.y - 1.0 / g_v2TexSize.y);
    float4 bkColor = float4(0.5, 0.5, 0.5, 1.0);
    float4 curColor = g_texture.Sample(g_sampler, input.m_v2UV);
    float4 upLeftColor = g_texture.Sample(g_sampler, upLeftUV);

    float4 delColor = curColor - upLeftColor;

    float h = 0.3 * delColor.x + 0.59 * delColor.y + 0.11 * delColor.z;
    float4 _outColor = float4(h, h, h, 0.0) + bkColor;
    return _outColor;
}

在上面的代码中我们首先计算得到了将要采样的纹理像素点的左上角像素采样点的归一化坐标，然后，两个Sample采样方法取得了两点的颜色值，接着计算出采样点与其左上角像素的颜色差，在以此颜色根据我们之前介绍的计算颜色亮度的方法，计算出亮度值，接着形成一个灰度颜色值，再跟背景灰度颜色相加形成最终采样点的颜色。

结合之前的知识，这个函数很好理解。还需要大家注意的一点就是[0,255]范围的颜色值在映射到[0.0-1.0]的归一化颜色空间中时，128颜色值对应的就是0.5这一归一化颜色值，对应关系就是：颜色值/255即可。这个也很好理解。其实由此也可以看出在我们的Shader编程中经常要用到这种归一化的坐标系（广义坐标系，理解为归一化的线性空间最好，或者称之为标准化向量）。当然这主要是因为我们通常将渲染目标的像素格式设置为UNORM形式，其含义就是unsigned normalize（无符号标准化/归一化）。

最终浮雕效果运行效果如下：

 

图中我们看到地球的显示效果类似于海洋干涸后的样子。

6、马赛克效果

马赛克（Mosaic）效果就是把图片的一个指定大小的区域用同一个点的颜色来表示。目的是大规模的降低图像的分辨率,而让图像的一些细节隐藏起来。（因为有些细节从此无法分辨，也被称为“万恶的马赛克”）。

用Shader代码实现马赛克是非常简单的。

第一步就是先把纹理坐标转换成像素坐标（前一节我们已经学习过该方法）。接下来要把图像这个坐标量化—比如马赛克块的大小是8×8像素。那么我们可以用下列方法来得到马赛克后的图像采样值，假设[x，y]为图像的像素坐标：

mosaic[X,Y] = [int(x/8) * 8 , int(y/8) * 8]

式中8可以是参数量的大小，在我们的Shader代码中就是应用一个全局的static型变量存储了这个参数的大小。前面的章节中我们也介绍了这个变量。

公式中int函数实际上截断了小数部分，因此马赛克大小范围内的像素点取整后的值都是左上角像素点的坐标。

得到这个坐标后只要用相反的方法，把坐标归一化到[0,1.0]的纹理坐标。

由此我们可以实现方形马赛克效果函数如下：

static float2 g_v2MosaicSize1 = float2(32.0f, 32.0f);
float4 Mosaic1(PSInput input)
{//方形马赛克
    float2 v2PixelSite
        = float2(input.m_v2UV.x * g_v2TexSize.x
            , input.m_v2UV.y * g_v2TexSize.y);

    float2 v2NewUV
        = float2(int(v2PixelSite.x / g_v2MosaicSize1.x) * g_v2MosaicSize1.x
            , int(v2PixelSite.y / g_v2MosaicSize1.y) * g_v2MosaicSize1.y);

    v2NewUV /= g_v2TexSize;
    return g_texture.Sample(g_sampler, v2NewUV);
}

代码逻辑很简单，也很好理解，就不再赘述了。

方形马赛克运行效果图如下（注意我将马赛克大小设置为32*32）：

 

方形的马赛克实现很简单，进一步我们可以实现稍微复杂一点的圆形马赛克。

首先求出原来马赛克区域的正中心（原来是左上角）：然后计算图像采样点到这个中心的距离，如果在马赛克圆内，就用区域的中心颜色，否则就用原来的颜色。改良后的代码如下，这里把马赛克区域大小调节成16×16。这样效果更明显。

static float2 g_v2MosaicSize2 = float2(16.0f, 16.0f);
float4 Mosaic2(PSInput input)
{//圆形马赛克
    float2 v2PixelSite
        = float2(input.m_v2UV.x * g_v2TexSize.x
            , input.m_v2UV.y * g_v2TexSize.y);

    //新的纹理坐标取到中心点
    float2 v2NewUV
        = float2(int( v2PixelSite.x / g_v2MosaicSize2.x) * g_v2MosaicSize2.x
            , int(v2PixelSite.y / g_v2MosaicSize2.y) * g_v2MosaicSize2.y)
        + 0.5 * g_v2MosaicSize2;

    float2 v2DeltaUV = v2NewUV - v2PixelSite;
    float fDeltaLen = length(v2DeltaUV);

    float2 v2MosaicUV = float2( v2NewUV.x / g_v2TexSize.x,v2NewUV.y / g_v2TexSize.y );
    float4 c4Color;
    //判断新的UV点是否在圆心内
    if ( fDeltaLen < 0.5 * g_v2MosaicSize2.x )
    {
        c4Color = g_texture.Sample(g_sampler, v2MosaicUV);
    }
    else
    {
        c4Color = g_texture.Sample(g_sampler, input.m_v2UV);
    }
    return c4Color;
}

上面的代码逻辑已经很清晰了，只是需要注意的是else分支中的Sample采样调用可能会被浪费了，因为它在圆外，有可能在临近的圆内，这时又会重采样为它所在的圆的圆心处的颜色。当然不在任何圆内的点就显示为原来的纹理颜色。

大家可以仿照这一思路继续发挥，可以编写比如“三角形”，“六边形”等的马赛克滤镜。

最终圆形马赛克运行效果如下：

 

最后需要提醒大家的是，因为纹理的坐标都被归一化到了[0,1.0]区间，而每个纹理又是不同的像素大小，所以对于最终马赛克的显示大小是不同的，这一点一定要注意。如果要显示的马赛克大小一致，那么就必须保证所有纹理的原始像素大小必须保持一致，大家可以使用图像编辑工具改变这几个纹理的原始大小为同一个尺寸运行后看看效果。

7、图像数字滤波

接下来我们要介绍稍微复杂一点的效果，第一个就是图像的模糊和锐化。

图像的模糊又成为图像的平滑(smoothing)，人眼对高频成分是非常敏感的。如果在一个亮度连续变化的图像中，突然出现一个亮点，那么我们很容易察觉出来。类似的，如果图像有个突然的跳跃—明显的边缘，我们也是很容易察觉出来的。这些突然变化的分量就是图像的高频成分。人眼通常是通过低频成分来辨别轮廓，通过高频成分来感知细节的（这也是为什么照片分辨率低的时候，人们只能辨认出照片的大概轮廓，而看不到细节）。但是这些高频成分通常也包含了噪声成分。图像的平滑处理就是滤除图像的高频成分。

那么如何才能滤除图像的高频成分呢？先来介绍一下图像数字滤波器的概念。

简单通俗的来说，图像的数字滤波器其实就是一个n*n的数组（数组中的元素成为滤波器的系数或者滤波器的权重，n称为滤波器的阶）。对图像做滤波的时候，把某个像素为中心的n*n个像素（“九宫格”）的值和这个滤波器做卷积运算（也就是对应位置上的像素和对应位置上的权重的乘积累加起来），公式如下：

其中x , y 为当前正在处理的像素坐标。

通常情况下，滤波器的阶数为3已经足够了，用于普通模糊处理的3*3滤波器如下:

经过这样的滤波器，其实就是等效于把一个像素和周围8个像素一起求平均值，这是非常合理的—等于把一个像素和周围几个像素搅拌在一起—自然就模糊了。

基于这个原理，我们先定义一个3*3滤波Shader函数如下：

float4 Do_Filter(float3x3 mxFilter,float2 v2UV,float2 v2TexSize, Texture2D t2dTexture)
{//根据滤波矩阵计算“九宫格”形式像素的滤波结果的函数
    float2 v2aUVDelta[3][3]
        = {
            { float2(-1.0f,-1.0f), float2(0.0f,-1.0f), float2(1.0f,-1.0f) },
            { float2(-1.0f,0.0f),  float2(0.0f,0.0f),  float2(1.0f,0.0f)  },
            { float2(-1.0f,1.0f),  float2(0.0f,1.0f),  float2(1.0f,1.0f)  },
        };

    float4 c4Color = float4(0.0f, 0.0f, 0.0f, 0.0f);
    for (int i = 0; i < 3; i++)
    {
        for (int j = 0; j < 3; j++)
        {
            //计算采样点，得到当前像素附件的像素点的坐标（上下左右，八方）
            float2 v2NearbySite
                = v2UV + v2aUVDelta[i][j];
            float2 v2NearbyUV
                = float2(v2NearbySite.x / v2TexSize.x, v2NearbySite.y / v2TexSize.y);
            c4Color += (t2dTexture.Sample(g_sampler, v2NearbyUV) * mxFilter[i][j]);
        }
    }
    return c4Color;
}

在上面代码中，我们首先定义了一个以像素为单位的偏移矩阵，即指定了上下左右八个方向的像素坐标偏移向量矩阵。如果需要更高阶的滤波，那么可以扩展这个矩阵，并且将循环中的次数修改为更高阶即可。基于这种思路，大家有兴趣可以试着实现一个4阶或更高阶的滤波函数来看下效果。

8、模糊滤波器（Box模糊和高斯模糊）

有了核心的滤波函数，我们首先来实现一个普通的模糊滤波器，也被称为BOX滤波器，是最简单的模糊滤波器，即中心像素取周边像素的平均值，其代码如下：

float4 BoxFlur(float2 v2UV,float2 v2TexSize)
{//简单的9点Box模糊
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);
    float3x3 mxOperators
        = float3x3(1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f
                    , 1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f
                    , 1.0f / 9.0f, 1.0f / 9.0f, 1.0f / 9.0f);
    return Do_Filter(mxOperators, v2PixelSite, v2TexSize, g_texture);
}

其运行效果如下：

如果考虑到离开中心像素的距离对滤波器系数的影响，我们通常采用更加合理的滤波器—高斯滤波器——一种通过2维高斯采样得到的滤波器，它的滤波矩阵如下：

很容易看出来，离开中心越远的像素，权重系数越小（对角线总是长于边长）。其代码实现如下：

float4 GaussianFlur(float2 v2UV, float2 v2TexSize)
{//高斯模糊
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);

    float3x3 mxOperators
        = float3x3(1.0f / 16.0f, 2.0f / 16.0f, 1.0f / 16.0f
            , 2.0f / 16.0f, 4.0f / 16.0f, 2.0f / 16.0f
            , 1.0f / 16.0f, 2.0f / 16.0f, 1.0f / 16.0f);

    return Do_Filter(mxOperators, v2PixelSite, v2TexSize, g_texture);
}

运行后效果如下：

从两个模糊效果来看，几乎看不出有什么差别，尤其与原图比较也没有较大的变化，这主要是这么几个原因：1、一般用于3D场景的纹理都经过了“去噪”处理，实际就是去高频滤波，有点类似于我们这里进行的模糊处理；2、我们的滤波还只是简单的3阶，要更加模糊的效果就需要更高阶的模糊处理；3、因为人类的视觉习惯，我们实际对低频的画面变化不敏感，这样本就没有多少高频成分的画面经过滤波后基本看不出太大变化；所以大家可以通过修改纹理（加入高频噪声）或者实现更高阶的滤波函数来改进这个模糊效果。

9、锐化效果（拉普拉斯锐化）

对于锐化操作，常用的锐化滤波算子是拉普拉斯(Laplacian)锐化算子，这个滤波算子矩阵定义如下：

容易看出拉普拉斯矩阵算子的操作如下：先将自身与周围的8个象素相减，表示自身与周围象素的差别；再将这个差别加上自身作为新象素的灰度。如果一片暗区出现了一个亮点，那么锐化处理的结果是这个亮点变得更亮，这就增强了图像的细节。

据此实现Shader函数如下：

float4 LaplacianSharpen(float2 v2UV, float2 v2TexSize)
{//拉普拉斯锐化
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);

    float3x3 mxOperators
        = float3x3(-1.0f, -1.0f, -1.0f
            , -1.0f, 9.0f, -1.0f
            , -1.0f, -1.0f, -1.0f);
    return Do_Filter(mxOperators, v2PixelSite, v2TexSize, g_texture);
}

其运行效果如下：

从图中可以明显看出多了很多“亮点”噪声，色彩对比度也有很大提升，轮廓部分也很清晰。大家可以修改拉普拉斯算子矩阵中间位置的值，适当调低，可以得到一个较满意的“锐化”滤镜效果。

通过这些效果，我们介绍了图像的滤波操作，这样的操作，也称为模板操作。它实现了一种邻域运算(Neighborhood Operation)，即某个像素点的结果灰度不仅和该像素灰度有关，而且和其邻域点的值有关。模板运算在图像处理中经常要用到，可以看出这是一项非常耗时的运算。有一种优化的方法称为可分离式滤波，就是使用两个pass来进行x/y方向分别滤波，能让运算次数大大减少。而且滤波器阶数越高，优势越明显。

数字图像滤波的时候，同样还需要注意边界像素的问题，不过幸好，HLSL能让边界处理更加的透明和简单（之前讲的在Sample上设置边界连续的采样器属性）。

10、描边

利用滤波函数，我们可以实现一种比浮雕效果更好效果的称之为描边的效果，描边（边缘检测）的代码并不复杂多少，只是在理论上相对来说稍微复杂一点，而且效果看上去更加的“顺眼”一些。

如果在图像的边缘处，灰度值肯定经过一个跳跃，我们可以计算出这个跳跃，并对这个值进行一些处理，从而得到边缘浓黑的描边效果。

首先考虑对这个象素的左右两个象素进行差值，得到一个差量，这个差量越大，表示图像越处于边缘，而且这个边缘应该左右方向的。同样我们能得到上下方向和两个对角线上的图像边缘。这样我们需要构造一个如下的滤波器矩阵算子：

经过这个滤波器后得到的是图像在这个像素处的变化差值，把它转化成灰度值并求绝对值（差值可能为负），然后我们定义差值的绝对值越大的地方越黑（边缘显然是黑的），否则越白。其代码实现如下：

float4 Contour(float2 v2UV, float2 v2TexSize)
{//描边
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);
    float3x3 mxOperators
        = float3x3(-0.5f, -1.0f, 0.0f
            , -1.0f, 0.0f, 1.0f
            , -0.0f, 1.0f, 0.5f);

    float4 c4Color = Do_Filter(mxOperators, v2PixelSite, v2TexSize, g_texture);

    float fDeltaGray = 0.3f * c4Color.x + 0.59 * c4Color.y + 0.11 * c4Color.z;

    //fDeltaGray += 0.5f;

    //OR

    if (fDeltaGray < 0.0f)
    {
        fDeltaGray = -1.0f * fDeltaGray;
    }
    fDeltaGray = 1.0f - fDeltaGray;

    return float4(fDeltaGray, fDeltaGray, fDeltaGray, 1.0f);
}

代码中逻辑很清晰了，只是最后计算得到亮度值后的处理，使用了与浮雕效果不同的方法，大家可以恢复被注释的代码，并注释后面这个if判断及1.0- fDeltaGray的语句看看效果，并与浮雕效果进行比较看看差异。

上面的效果运行效果如下：

从图中可以看到一些高频噪点，大家可以分析下为什么会出现这样的情况，有什么方法可以补救？

11、索贝尔滤波算子（Sobel，或译作索伯尔）

上面演示的效果中用到的滤波矩阵算子就是一种边缘检测器，在信号处理上是一种基于梯度的滤波器，又称边缘算子。梯度（实际就是向量的导数）是有方向的，和边沿的方向总是正交(垂直)的，在上面的代码中，我们采用的就是一个梯度为45度方向模板（注意其中偏移像素的权重取值和正负号），它可以检测出135度方向的边沿。

更加严格的，我们可以采用Sobel算子。Sobel 算子有两个，一个是检测水平边沿的，另一个是检测垂直平边沿的，如下：

同样，Sobel算子另一种形式是各向同性Sobel算子，也有两个，一个是检测水平边沿的，另一个是检测垂直边沿的：

各向同性Sobel算子和普通Sobel算子相比，它的位置加权系数更为准确，在检测不同方向的边沿时梯度的幅度一致。

为了综合展示垂直和水平方向上的Sobel算子效果，在示例Shader代码中，特意将两个方向计算的结果进行了相加处理，代码实现如下：

float4 SobelAnisotropyContour(float2 v2UV, float2 v2TexSize)
{//各向异性索博尔描边
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);
    float3x3 mxOperators1
        = float3x3(  -1.0f, -2.0f, -1.0f
                    , 0.0f, 0.0f, 0.0f
                    , 1.0f, 2.0f, 1.0f
                  );

    float3x3 mxOperators2
        = float3x3(  -1.0f, 0.0f, 1.0f
                    ,-2.0f, 0.0f, 2.0f
                    ,-1.0f, 0.0f, 1.0f
                  );

    float4 c4Color1 = Do_Filter(mxOperators1, v2PixelSite, v2TexSize, g_texture);
    float4 c4Color2 = Do_Filter(mxOperators2, v2PixelSite, v2TexSize, g_texture);

    c4Color1 += c4Color2;

    float fDeltaGray = 0.3f * c4Color1.x + 0.59 * c4Color1.y + 0.11 * c4Color1.z;

    if (fDeltaGray < 0.0f)
    {
        fDeltaGray = -1.0f * fDeltaGray;
    }
    fDeltaGray = 1.0f - fDeltaGray;

    return float4(fDeltaGray, fDeltaGray, fDeltaGray, 1.0f);

}

float4 SobelIsotropyContour(float2 v2UV, float2 v2TexSize)
{//各向同性索博尔描边
    float2 v2PixelSite
        = float2(v2UV.x * v2TexSize.x, v2UV.y * v2TexSize.y);
    float3x3 mxOperators1
        = float3x3(  -1.0f, -1.414214f, -1.0f
                    , 0.0f, 0.0f, 0.0f
                    , 1.0f, 1.414214f, 1.0f
                    );

    float3x3 mxOperators2
        = float3x3(   -1.0f, 0.0f, 1.0f
                    , -1.414214f, 0.0f, 1.414214f
                    , -1.0f, 0.0f, 1.0f
                    );

    float4 c4Color1 = Do_Filter(mxOperators1, v2PixelSite, v2TexSize, g_texture);
    float4 c4Color2 = Do_Filter(mxOperators2, v2PixelSite, v2TexSize, g_texture);

    c4Color1 += c4Color2;

    float fDeltaGray = 0.3f * c4Color1.x + 0.59 * c4Color1.y + 0.11 * c4Color1.z;

    if (fDeltaGray < 0.0f)
    {
        fDeltaGray = -1.0f * fDeltaGray;
    }
    fDeltaGray = 1.0f - fDeltaGray;

    return float4(fDeltaGray, fDeltaGray, fDeltaGray, 1.0f);
}

代码中对于根号2取了其有限近似值，代码中的逻辑也很清晰，为了查看不同方向上的实际效果，建议大家注释某一个方向的计算代码，只保留另一个方向的计算看看实际效果。当然也可以采用浮雕中的加上固定背景色的方法来看看是什么效果。

这两个效果运行效果如下：

上图是各向异性的效果。下图是各向同性的效果：

实际上可以发现两个效果区别不是很明显，这主要是因为二者实际矩阵算子中的因子差异不是很大，一个是2，另一个是1.414，几乎已经看不出什么差别了。

最后提示大家注意的就是，我们的几个效果函数最后处理灰度值的时候，使用了负值直接变正值，然后用1减去亮度值的方法，其实严格来说这个方法是不正确的，因为这里没有考虑溢色问题，即颜色值超出了[0,1]^3范围外的问题，这时正确的做法应该是取所有颜色分量的最小最大范围区间[min,max],然后用(溢色颜色值-min)/(max-min)进行正确归一化,即进行全景的HDR映射计算（实际压缩了图像细节的亮度、对比度等）。但这对一般的实时图像处理来说代价太大，因为要遍历一副渲染图中所有的颜色值，所以一般采用较简单的处理方法，即取计算所得的颜色值中的分量来做映射归一化计算，代码示例如下：

//计算颜色溢色的简单方法
float fMaxColorComponent
    = max(c4Color1.x
    , max(c4Color1.y
        , c4Color1.z));
float fMinColorComponent
    = min(
    min(c4Color1.x
        , min(c4Color1.y
            , c4Color1.z))
    ,0.0f);

c4Color1 = (c4Color1 - float4(fMinColorComponent
    , fMinColorComponent
    , fMinColorComponent
    , fMinColorComponent))
    /(fMaxColorComponent- fMinColorComponent);

在各向异性的索伯尔算子的代码中，我加入了这段代码，并注释了。大家可以自行还原，然后注释后面的if判断及1-亮度值语句后看看效果。

当然对于实时渲染来说，这样的溢色处理基本足够了。这个方法很重要建议大家能够理解并记忆。最好能够将这个溢色处理过程封装到Shader函数库，以供将来使用。（在后续的Raytracing Shader教程中任然会用到这个方法）。

12、后记

细心的网友肯定发现这一章教程是不完整的，因为至少示例代码中的水彩画的效果还没有讲解，其实直到我写这篇文章时，我才发现水彩画效果其实是有问题的，因为少了一遍高斯模糊处理，所以必须要回炉再造，并且加上这个“后处理”才算正确，所以我打算放在后面一章再讲解。另外还有一个伪HDR效果也没有讲解，因为当时我以为现在伪HDR没啥用了，后来我发现是我自个估计错了，同时这个效果可能是解决前面讲的“溢色”问题的另一个思路，所以考虑下一章将它也补充进来。

敬请期待！