This series of articles are the study notes of " Machine Learning ", by Prof. Andrew Ng., Stanford University. This article is the notes of week 5, Neural Networks Learning. This article contains some topic about how to apply Backpropagation algorithm in practice.

Backpropagation in Practice

1. Implementation note: Unrolling parameters

Advanced optimization 

        function [jVal, gradient] =costFunction(theta)

           …

        optTheta = fminunc(@costFunction, initialTheta,options)

Neural Network (L=4):

“Unroll” into vectors

Example

        thetaVec = [ Theta1(:);Theta2(:); Theta3(:)];

        DVec = [D1(:); D2(:); D3(:)];

      Theta1 =reshape(thetaVec(1:110),10,11);

        Theta2 =reshape(thetaVec(111:220),10,11);

        Theta3 = reshape(thetaVec(221:231),1,11); 

Learning Algorithm 

2. Gradient checking

There may be bugs in back prop

In the last few videos we talked about how to do forward propagation and back propagation in a neural network in order to compute derivatives. But back prop as an algorithm has a lot of details and can be a little bit tricky to implement. And one unfortunate property is that there are many ways to have subtle bugs in back prop. So that if you run it with gradient descent or some other optimization algorithm, it could actually look like it's working. And your cost function, J of theta may end up decreasing on every iteration of gradient descent. But this could prove true even though there might be some bug in your implementation of back prop. So that it looks J of theta is decreasing, but you might just wind up with a neural network that has a higher level of error than you would with a bug free implementation.

Gradient checking eliminates the bugs

So, what can we do about this? There's an idea called gradient checking that eliminates almost

all of these problems. So, today every time I implement back propagation or a similar gradient descent algorithm on a neural network or any other reasonably complex model, I always implement gradient checking. And if you do this, it will help you make sure and sort of gain high confidence that your implementation of forward prop and back prop or whatever is 100% correct.
And in the previous videos I asked you to take on faith that the formulas I gave for computing the deltas and the vs and so on, I asked you to take on faith that those actually do compute the gradients of the cost function. But once you implement numerical gradient checking, which is the topic of this section, you'll be able to absolute verify for yourself that the code you're writing is indeed computing the derivative of the cost function J.

Gradient checking

So here's the idea, consider the following example. Suppose that I have the function J(θ) and I have some value theta and for this example gonna assume that theta is just a real number. 

And let's say that I want to estimate the derivative of this function at this point and so the derivative is equal to the slope of that tangent one. Here's how I'm going to numerically approximate the derivative, or rather here's a procedure for numerically approximating the derivative. I'm going to compute theta plus epsilon, so now we move it to the right. And I'm gonna compute theta minus epsilon and I'm going to look at those two points, And connect them by a straight line And I'm gonna connect these two points by a straight line, and I'm gonna use the slope of that little red line as my approximation to the derivative. Which is, the true derivative is the slope of that blue line over there. So, you know it seems like it would be a pretty good approximation. Mathematically, the slope of this red line is this vertical height divided by this horizontal width.

Implement:

          gradApprox = (J(theta + EPSILON) – J(theta – EPSILON)) /(2*EPSILON)

Parameter vector θ

for i = 1:n,

        thetaPlus = theta;

        thetaPlus(i) = thetaPlus(i) + EPSILON;

       thetaMinus = theta;

       thetaMinus(i) = thetaMinus(i) – EPSILON;

        gradApprox(i) = (J(thetaPlus) – J(thetaMinus))

                              /(2*EPSILON);

end;

Check that： gradApprox ≈ DVec 

Implementation Note: 

        –    Implement backprop to compute DVec (unrolled D⁽¹⁾,D⁽²⁾ , D⁽³⁾).

        –    Implement numerical gradient check to compute gradApprox.

        –    Make sure they give similar values.

        –    Turn off gradient checking. Using backprop code for learning.

Important:

        –    Be sure to disable your gradient checking code before training
your classifier. If you run numerical gradient computation on
every iteration of gradient descent (or in the inner loop of cost Function(…))your code will be very slow.

3. Random initialization

In the previous video, we've put together almost all the pieces you need in order to implement and train in your network. There's just one last idea I need to share with you, which is the idea of
random initialization. When you're running an algorithm of gradient descent, or also the advanced optimization algorithms, we need to pick some initial value for the parameters theta.
So for the advanced optimization algorithm, it assumes you will pass it some initial value for the parameters theta.

What can we set the initial value of theta?

Now let's consider a gradient descent. For that, we'll also need to initialize theta to something, and then we can slowly take steps to go downhill using gradient descent. To go downhill, to minimize the function j of theta. So what can we set the initial value of theta to?

Initial value of θ

For gradient descent and advanced optimization method, need initial value for θ .

        optTheta = fminunc(@costFunction,

                                      initialTheta, options)

Zero initialization

Consider gradient descent

Set initialTheta =zeros(n,1) ?

Is it possible to set the initial value of theta to the vector of all zeros? Whereas this worked OK when we were using logistic regression,initializing all of your parameters to zero actually does not work when you are trading on your own network.

Consider trading the follow Neural network, and let's say we initialize all the parameters of the network to 0.

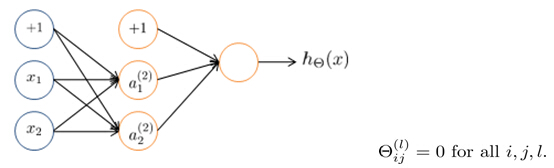
After each update, parameters corresponding to inputs going into each of two hidden units are identical: a₁⁽²⁾ , a₂⁽²⁾ 

And if you do that, then what you, what that means is that at the initialization, this blue weight, colored in blue is gonna equal to that weight, so they're both 0. And this weight that I'm coloring in in red, is equal to that weight, colored in red, and also this weight, which I'm coloring in green is going to equal to the value of that weight. And what that means is that both of your hidden units, A1 and A2, are going to be computing the same function of your inputs. And thus you end up with for every one of your training examples, you end up with a₁⁽²⁾ =a₂⁽²⁾ . And moreover because I'm not going to show this in too much detail, but because these outgoing weights are the same you can also show that the delta values are also gonna be the same.

the two blue waves, will stay the same as each other. The two red waves will stay the same as each other and the two green waves will stay the same as each other.

Imagine that you had not only two hidden units, but imagine that you had many, many hidden units. Then what this is saying is that all of your headed units are computing the exact same feature. All of your hidden units are computing the exact same function of the input. And this is a highly redundant representation because you find the logistic progression unit. It really has to see only one feature because all of these are the same. And this prevents you and your network from doing something interesting.

Random initialization: Symmetry breaking 

Concretely, the problem was saw on the previous slide is something called the problem of symmetric ways, that's the ways are being the same. So this random initialization is how we perform symmetry breaking. So what we do is we initialize each value of theta to a random number between minus epsilon and epsilon.

Initialize each  θ_ij^(l) to a random value in [-ε, ε]

    i.e. –ε≤θ_ij^(l) ≤ε

The way I write code to do this in octave or matlab is below

E.g.

        Theta1 =  rand(10,11)*(2*INIT_EPSILON)- INIT_EPSILON;

        Theta2 = rand(1,11)*(2*INIT_EPSILON) – INIT_EPSILON;

This ε here has nothing to do with the ε that we were using when we were doing gradient checking. So when numerical gradient checking, there we were adding some values of epsilon and theta. This is your unrelated value of epsilon. We just wanted to notate init epsilon just to distinguish it from the value of epsilon we were using in gradient checking.

Summarize

So to summarize, to create a neural network what you should do is randomly initialize the waves

to small values close to zero, between -ε and +ε say. And then implement back propagation, do great in checking, and use either great in descent or 1b advanced optimization algorithms to try to minimize J(θ) as a function of the parameters θ starting from just randomly chosen initial value for the parameters. And by doing symmetry breaking, which is this process, hopefully great gradient descent or the advanced optimization algorithms will be able to find a good value of θ.

4. Putting It Together

So, it's taken us a lot of sections to get through the neural network learning algorithm. In this section, what I'd like to do is try to put all the pieces together, to give a overall summary or a bigger picture view, of how all the pieces fit together and of the overall process of how to implement a neural network learning algorithm.

Training a neural network 

Pick some network architecture

When training a neural network, the first thing you need to do is pick some network architecture and by architecture I just mean connectivity pattern between the neurons.


Pick a network architecture (connectivity pattern between neurons) 

    –    No. of input units: Dimension of features x⁽ⁱ⁾

    –    No.output units: Number of classes

    –    Reasonable default: 1 hidden layer, or if >1 hidden layer, have same no. of hidden units in every layer (usually the more the better) 

And as for the number of hidden units and the number of hidden layers, a reasonable default is to use a single hidden layer and so this type of neural network shown on the left with just one hidden layer is probably the most common. Or if you use more than one hidden layer, again the reasonable default will be to have the same number of hidden units in every single layer. So here we have two hidden layers and each of these hidden layers have the same number five of hidden units and here we have, you know, three hidden layers and each of them has the same number, that is five hidden units. Rather than doing this sort of network architecture on the left would be a perfect ably reasonable default. And as for the number of hidden units – usually, the more hidden units the better; it's just that if you have a lot of hidden units, it can become more computationally expensive, but very often, having more hidden units is a good thing. And usually the number of hidden units in each layer will be maybe comparable to the dimension of x, comparable to the number of features, or it could be any where from same number of hidden units of input features to maybe so that three or four times of that. So having the number of hidden units is comparable. 

Training a neural network 

【5】So, I do gradient checking to make sure that both of these give you very similar values. Having done gradient checking just now reassures us that our implementation of back propagation is correct, and is then very important that we disable gradient checking, because the gradient checking code is computationally very slow. And finally, we then use an optimization algorithm such as gradient descent, or one of the advanced optimization methods such as LB of GS, contract gradient has embodied into fminunc or other  optimization methods. We use these together with back propagation, so back propagation is the thing that computes these partial derivatives for us.

【6】And so, we know how to compute the cost function, we know how to compute the partial derivatives using back propagation, so we can use one of these optimization methods to try to minimize j of theta as a function of the parameters theta. And by the way, for neural networks, this cost function J(θ) is non-convex, or is not convex and so it can theoretically be susceptible to local minimal, and in fact algorithms like gradient descent and the advance optimization methods can, in theory, get stuck in local optima, but it turns out that in practice this is not usually a huge problem and even though we can't guarantee that these algorithms will find a global optimum, usually algorithms like gradient descent will do a very good job minimizing this cost function J(θ) and get a very good local minimum, even if it doesn't get to the global optimum.

Gradient descents for a neural network

Finally, gradient descents for a neural network might still seem a little bit magical. So, let me just show one more figure to try to get that intuition about what gradient descent for a neural network is doing.

We have some cost function, and we have a number of parameters in our neural network. Right here I've just written down two of the parameter values. In reality, of course, in the neural network, we can have lots of parameters with these. We can have very high dimensional parameters but because of the limitations the source of parts we can draw. I'm pretending that we have only two parameters in this neural network.
Now, this cost function j of theta measures how well the neural network fits the training data. So, if you take a point like the red circle, down here, that's a point where J(θ) is pretty low, and so this corresponds to a setting of the parameters. There's a setting of the parameters theta, where, you know, for most of the training examples, the output of my hypothesis, that may be pretty close to y(i) and if this is true than that's what causes my cost function to be pretty low.

Whereas in contrast, if you were to take a value like the blue circle, a point like that corresponds to, where for many training examples,the output of my neural network is far from the actual value  y⁽ⁱ⁾. that was observed in the training set. So points like this on the line correspond to where the hypothesis, where the neural network is outputting values on the training set that are far from y⁽ⁱ⁾. So, it's not fitting the training set well.

What gradient descent does is going down hill repeatedly

So what gradient descent does is we'll start from some random initial point like that one in green circle there, and it will repeatedly go downhill. 

What back propagation does is computing the direction of the gradient

And so what back propagation is doing is computing  the direction of the gradient and what gradient descent is doing is it's taking little steps downhill until hopefully it gets to, in this case, a pretty good local optimum.