OPEN CASCADE Gauss Least Square
Abstract. The least square can be used to solve a set of n linear equations of m unknowns(n >= m). The OPEN CASCADE class math_GaussLeastSquare implements the least square solution of the linear equations by using Gauss LU decomposition algorithm. The paper focus on the Least Square method to solve the linear equations.
Key Words. Least Square, LU Decomposition, Linear Equations
1.Introduction
最小二乘(Least Square)问题是一类特殊的无约束优化问题,它在科学与工程计算中有十分重要的应用。最小二乘问题产生于数据拟合问题,它是一种基于观测数据与模型数据之间的差的平方和最小来估计模型参数的方法。它最早由德国数学家高斯Gauss于1794年,在预测行星轨道时提出,当时高斯只有17岁,后来得到广泛应用。
许多工程问题常常需要根据两个变量的几组实验数值来找出这两个变量的函数关系的近似表达式,通常把这样得到的函数的近似表达式称为经验公式。经验公式建立后就可以把生产或实验中所积累的某些经验提高到理论上加以分析。
在几何造型中常常需要对曲线和曲面进行拟合(插值和逼近),根据一些采样点来拟合曲线曲面。逼近比插值更为困难。在插值问题中,只是根据采样点来建立方程组,直接求解方程组即可得到结果,不需要进行容差检查。而在逼近问题中,容差和采样点一起作为输入,一般预先不知道需要多少个控制点才能达到预期的精度,因此逼近一般都需要通过迭代来实现。通过最小二乘法即可实现达到精度要求的拟合结果,如OPEN CADCADE中的曲线曲面逼近就采用了最小二乘算法。
本文主要关注于最小二乘法求解线性方程组的原理及OPEN CASCADE中的实现和用法,为探索最小二乘法在OPEN CASCADE曲线曲面拟合方面的应用提前做些热身准备。最小二乘问题涉及到非线性最优化的相关知识,对多元函数的微积分有些要求,可以找出原来的《高等数学》或《数学分析》的课本复习下。本文关注的应用最小二乘法求解线性方程组问题只涉及到线性代数或矩阵相关的知识。
2.Principle
在罗家洪、方卫东编著的《矩阵分析引论》一书中的2.5节点到子空间距离与最小二乘法,用欧氏空间的概念来表达最小二乘法,并给出最小二乘解所满足的代数条件的证明过程。本文摘抄主要内容对最小二乘法求解线性方程组的理解。
设已给不相容实系数线性方程组(即无解的线性方程组):
因为这方程组无解,设法找出一组数x1’, x2’, …, xn’使平方偏差最小:
这组数称为此方程组的最小二乘解,这一方法叫做最小二乘法。经证明,最小二乘解所满足的代数方程为:
它是一个线性方程组,系数矩阵为ATA,常数项为ATB。使用上述结论来解如下线性方程组:
由于:
所以:
于是求得最小二乘解为:x1=17/6, x2=-13/6, x3=-4/6。
在OPEN CASCADE的数据工具集中TKMath,使用类math_GaussLeastSquare来利用最小二乘法来对线性方程组进行求解。其实现代码如下所示:
math_GaussLeastSquare::math_GaussLeastSquare (const math_Matrix& A, const Standard_Real MinPivot) : LU(1, A.ColNumber(), 1, A.ColNumber()), A2(1, A.ColNumber(), 1, A.RowNumber()), Index(1, A.ColNumber()) { A2 = A.Transposed(); LU.Multiply(A2, A); Standard_Integer Error = LU_Decompose(LU, Index, D, MinPivot); Done = (!Error) ? Standard_True : Standard_False; } void math_GaussLeastSquare::Solve(const math_Vector& B, math_Vector& X) const{ StdFail_NotDone_Raise_if(!Done, \" \"); Standard_DimensionError_Raise_if((B.Length() != A2.ColNumber()) || (X.Length() != A2.RowNumber()), \" \"); X.Multiply(A2, B); LU_Solve(LU, Index, X); return; }
结合上述公式,再来理解这个代码实现的思路还是很清晰的。
3.Code Example
OPEN CASCADE的TKMath工具集中提供了类math_GaussLeastSquare实现了使用高斯LU分解算法求m个未知数的n个线性方程组的最小二乘解,其中n>=m。下面给出使用类math_GaussLeastSquare对上述线性方程组进行求解的示例程序:
/* * Copyright (c) 2015 Shing Liu All Rights Reserved. * * File : main.cpp * Author : Shing Liu(eryar@163.com) * Date : 2015-11-25 21:00 * Version : OpenCASCADE6.9.0 * * Description : Test Gauss Least Square method to * solve linear equations. */ #define WNT #include <math_GaussLeastSquare.hxx> #pragma comment(lib, \"TKernel.lib\") #pragma comment(lib, \"TKMath.lib\") void testLeastSquare(void) { math_Matrix A(1, 4, 1, 3); math_Vector B(1, 4); math_Vector X(1, 3); A(1,1) = 1.0; A(1,2) = 1.0; A(1,3) = 0.0; B(1) = 1.0; A(2,1) = 1.0; A(2,2) = 0.0; A(2,3) = 1.0; B(2) = 2.0; A(3,1) = 1.0; A(3,2) = 1.0; A(3,3) = 1.0; B(3) = 0.0; A(4,1) = 1.0; A(4,2) = 2.0; A(4,3) = -1.0; B(4) = -1.0; math_GaussLeastSquare aSolver(A); aSolver.Solve(B, X); if (aSolver.IsDone()) { std::cout << aSolver; std::cout << X; } } int main(int argc, char* argv[]) { testLeastSquare(); return 0; }
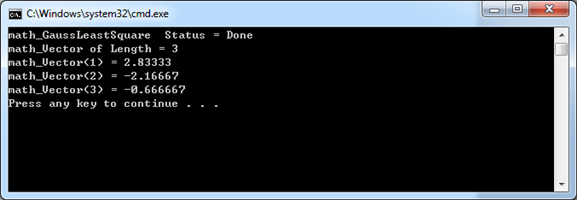
程序运行结果如下图所示:
由上图可知,计算结果吻合。
4.Conclusion
最小二乘法在系统理论中处理最小优化问题时有重要应用,本文主要关注于线性方程组的最小二乘法求解,且对方程个数与未知数个数不要求相等。最小二乘法也是在我们学习高等数学的多元函数微分后,提出的一个实用的函数公式拟合方法。虽然本文所述的最小二乘法主要用于方程组的求解,但是OPEN CASCADE中曲线曲面的逼近也是采用了最小二乘法,这里最小二乘法就涉及到非线性最优化的相关理论。
纵观OPEN CASCADE的数学工具集TKMath中,大量地用到了非线性最优化理论,如类math_BFGS就实现了Broyden-Fletcher-Goldfarb-Shanno(BFGS),用于计算多变量函数的最小值,类math_FRPR实现了Fletcher-Reeves-Polak-Ribiere算法。BFGS算法是拟牛顿方法,是解决无约束优化问题既快又稳定的算法。这些最优化算法广泛地用于OPEN CASCADE中曲线曲面拟合、光顺及求交等算法中。所以有必要对最优化方法,非线性最优化理论等知识进行学习。掌握一些最优化方法,不仅可以方便理解OPEN CASCADE中的核心关键算法,还可以将这些理论方法灵活应用在自己的程序中,提高软件质量。由于本人能力有限,先在这儿抛砖引玉,感兴趣的读者可以结合相关书籍对非线性最优化理论进行学习,研究,应用,创新。
5.References
1. 同济大学数学教研室. 高等数学. 高等教育出版社. 1996
2. 王仁宏. 李崇君. 朱春钢. 计算几何教程. 科学出版社. 2008
3. 罗家洪. 方卫东. 矩阵分析引论. 华南理工大学出版社. 2006
4. 易大义. 陈道琦. 数值分析引论. 浙江大学出版社. 1998
5. 赵罡. 穆国旺. 王拉柱. 非均匀有理B样条. 清华大学出版社. 2010
6. 王宜举. 修乃华. 非线性最优化理论与方法. 科学出版社. 2012
PDF Version: OPEN CASCADE Gauss Least Square
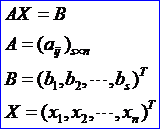

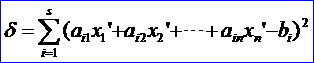
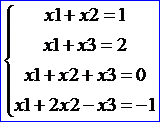



![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)












