计算几何05_B样条曲线

05356201

在这里插入图片描述

首先我们应该来了解一下为什么要有B样条曲线，主要原因是因为Bezier曲线的不足：

  • 1.确定了控制多边形的顶点个数，也就确定了曲线的次数；
  • 2.控制多边形与曲线的逼近程度较差，次数越高，逼进程度越差；
  • 3.曲线不能局部修改，调整某一控制点将影响到整条曲线，原因是伯恩斯坦基函数在整个[0,1]区间内有支撑，所以曲线在区间内任何一点的值都将受到全部顶点的影响，调整任何控制点的位置，将会引起整条曲线的改变；
  • 4.Bezier曲线的拼接比较复杂。

为了保留Bezier方法的优点，仍采用控制顶点定义曲线。改用B样条基函数代替伯恩斯坦基函数。舍恩伯格指出，B样条具有局部支撑性质。B样条基函数是多项式样条空间具有最小支撑的一组基函数，故也被称之为基本样条（Basis Spline），简称B样条（B-Spline）。

一、 B样条的递推定义

B样条的递推定义，常用de Boor-Cox递推公式如下：
在这里插入图片描述
具体的参数解释如下：
在这里插入图片描述
从上式中我们可以看出其通式符合递归条件，如下图基函数生成过程的三角阵列中所示；
在这里插入图片描述
举例如下：

1.1 零次B样条

当k=0时，由式可以直接给出零次B样条。
在这里插入图片描述
具体图形表示如下：
在这里插入图片描述
可以看出,零次B样条基函数Fi,o(t)在其定义区间上形状为一水平直线段。只在一个区间[ti,ti+i]上不为零,在其他子区间均为零。Fi,o(t)称为平台函数。

1.2 一次B样条

由Fi,o(t)移位，得到：
在这里插入图片描述
且根据公式：
在这里插入图片描述
结合以上两式，得：
在这里插入图片描述
图形表达上式如下：
在这里插入图片描述

1.3 二次B样条

二次B样条表达如下：
在这里插入图片描述
其计算过程：
在这里插入图片描述
其计算过程：

图形表达上式如下：
在这里插入图片描述

1.4 三次B样条

三次B样条表达如下
在这里插入图片描述
其计算过程：
在这里插入图片描述
带入，得：
在这里插入图片描述

图形表达上式如下：
在这里插入图片描述

1.5 B样条基函数性质

在这里插入图片描述

1.6 B样条基函数算法

1.6.1 代码实现

在这里插入图片描述

//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
double BasisFunctionValue(double t, int i, int k)
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

二、B样条曲线

2.1 B样条曲线定义

B样条曲线的数学定义为:
在这里插入图片描述
具体详释：
在这里插入图片描述
尤为注意的是：

B样条有三大要素：节点，控制点，阶次。
其中B样条曲线所对应的节点向量区间：u[uk-1,un+1]
其具体定义理解可参照B站教程：计算机图形学bezier曲线曲面B样条曲线曲面

根据节点向量中节点的分布可以将B样条曲线分为以下四类：均匀B样条曲线、准均匀B样条曲线、分段Bezier曲线和非均匀B样条曲线。

2.2 均匀B样条曲线

在这里插入图片描述

2.2.1 二次均匀B样条曲线

在这里插入图片描述

二次均匀B样条曲线的几何意义,如下图：
在这里插入图片描述

2.2.1.1 代码实现

CP2 P[6];//控制点
double knot[9];//节点数组
int n;//控制点数-1
int k;//次数
    
CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	knot[0]=-0.5,knot[1]=-0.25,knot[2]=0.0,knot[3]=0.25,knot[4]=0.5,knot[5]=0.75;//均匀二次B样条
	knot[6]= 1.0,knot[7]= 1.25,knot[8]= 1.5;
	n=5,k=2;
	P[0].x=-460,  P[0].y=-49;
	P[1].x=-355,  P[1].y=204;
	P[2].x= -63,  P[2].y=241;
	P[3].x= 66,   P[3].y=-117;
	P[4].x= 264,  P[4].y=-101;
	P[5].x= 400,  P[5].y=208;
}
void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);
	double tStep=0.05;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0,0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

在这里插入图片描述

2.2.2 三次均匀B样条曲线

在这里插入图片描述

三次均匀B样条曲线的几何意义,如下图：
在这里插入图片描述

2.2.2.1 代码实现

CP2 P[6];//控制点
double knot[11];//节点数组
int n;//控制点数-1
int k;//次数
    
CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	knot[0]=-3/3.0,knot[1]=-2/3.0,knot[2]=-1/3.0,knot[3]=0.0,knot[4]=1/3.0,knot[5]=2/3.0;//均匀三次B样条
	knot[6]=1.0,knot[7]= 4/3.0,knot[8]= 5/3.0,knot[9]=6/3.0;
	n=5,k=3;		
	P[0].x=-460,  P[0].y=-49;
	P[1].x=-355,  P[1].y=204;
	P[2].x= -63,  P[2].y=241;
	P[3].x= 66,   P[3].y=-117;
	P[4].x= 264,  P[4].y=-101;
	P[5].x= 400,  P[5].y=208;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);	
	double tStep=0.01;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0.0,0.0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

在这里插入图片描述

2.2.3 均匀B样条曲线灵活性

1.二重顶点
在曲线设计中，若要使B样条曲线与控制多边形的边相切，可使用二重点方法，如图所示。
2.三重顶点
要想在曲线中出现尖点，可使用三重点方法，如图所示。
在这里插入图片描述
3.三顶点共线
当三个顶点共线时，△P1P2P3退化为一段直线。可用于处理两段弧的相接。
在这里插入图片描述
4.四顶点共线
当四个顶点共线时，控制多边形P1P2P3 P4退化为一段直线，相应的B样条曲线段也退化为一段直线，可用于处理两段曲线之间接入一段直线的问题。
在这里插入图片描述
当控制多边形的首末端点全部为三重点，这可以使三次均匀B样条曲线过控制多边形的首末端点。
在这里插入图片描述

2.3 准均匀B样条曲线

均匀B样条的特点是节点等距分布，由各节点形成的B样条相同，可视为同一B样条的简单平移。均匀B样条基函数在[0, 1]区间上具有统一的表达式，使得计算与处理简单方便。一般情况下，应用均匀B样条可以获得满意的效果，而且计算效率高。但均匀B样条曲线有一个缺点，即未保留Bezier曲线的端点几何性质。曲线的首末端点不再是控制多边形的首末顶点。准均匀B样条曲线就是为了解决这个问题而提出的，目的是对曲线在端点的行为进行控制。

k次准均匀B样条曲线的节点矢量中，两端节点具有重复度k + 1，所有内节点呈均匀分布。因此，准均匀B样条曲线具有同次Bezier曲线的端点几何性质。两端节点k + 1重复度的出现，导致准均匀B样条曲线在计算与处理上，要比均匀B样条曲线复杂得多。实践中，是选择均匀B样条曲线还是选择准均匀B样条曲线，是需要斟酌的。

2.3.1 二次准均匀B样条曲线

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	knot[0]=0,knot[1]=0,knot[2]=0,knot[3]=1/4.0,knot[4]=2/4.0,knot[5]=3/4.0;//准均匀二次均匀B样条
	knot[6]=1,knot[7]=1,knot[8]=1;
	n=5,k=2;
	P[0].x=-460,  P[0].y=-49;
	P[1].x=-355,  P[1].y=204;
	P[2].x= -63,  P[2].y=241;
	P[3].x= 66,   P[3].y=-117;
	P[4].x= 264,  P[4].y=-101;
	P[5].x= 400,  P[5].y=208;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);	
	double tStep=0.01;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0.0,0.0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

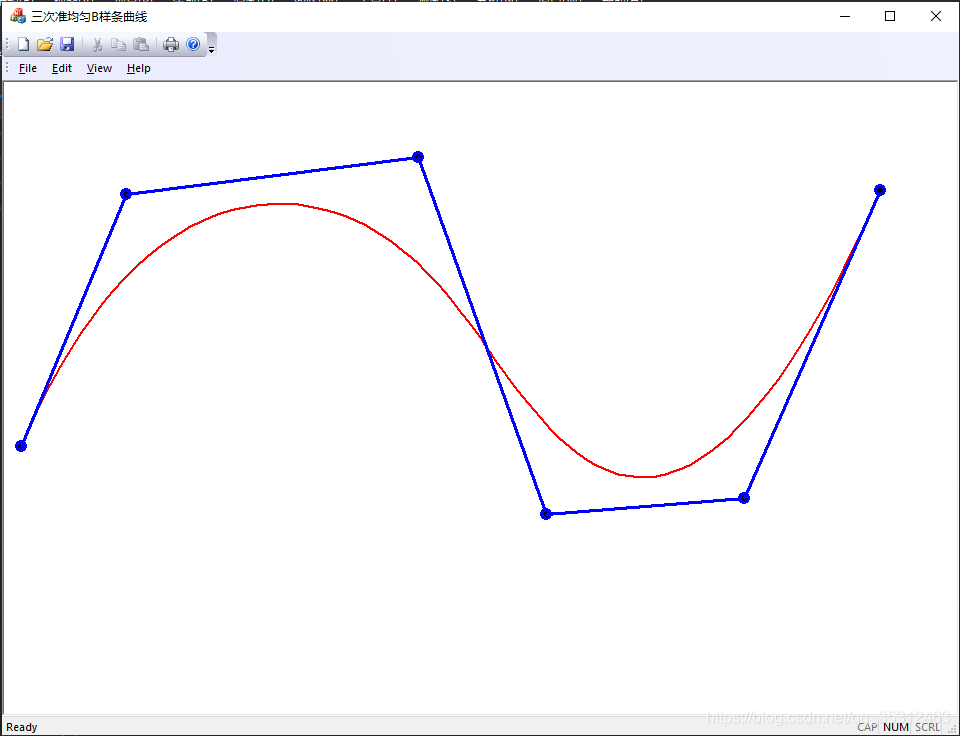
在这里插入图片描述

2.3.1 三次准均匀B样条曲线

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	knot[0]=0,knot[1]=0,knot[2]=0,knot[3]=0,knot[4]=1/3.0,knot[5]=2/3.0;//准均匀三次均匀B样条
	knot[6]=1,knot[7]=1,knot[8]=1,knot[9]=1;
	n=5,k=3;		
	P[0].x=-460,  P[0].y=-49;
	P[1].x=-355,  P[1].y=204;
	P[2].x= -63,  P[2].y=241;
	P[3].x= 66,   P[3].y=-117;
	P[4].x= 264,  P[4].y=-101;
	P[5].x= 400,  P[5].y=208;
}
void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);
	double tStep=0.01;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0.0,0.0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

在这里插入图片描述

2.4 分段Bezier曲线

分段Bezier是B样条曲线的一种特殊类型，是一组顺序首尾相接且同为k次的Bezier曲线。在STEP中是这样来表示的：节点矢量中首末端节点重复度取成k + 1，所有内节点取成重复度k。选用分段Bezier曲线有个限制条件：控制顶点数减1必须是次数的整数倍，即n/k = 正整数；否则不能生成曲线。即使满足整数倍要求，所生成的分段Bezier曲线在连接点处也只能达到C1连续性。分段Bezier的主要用途之一，就是把几何连续的分段多项式曲线统一采用B样条表示。

2.4.1 代码实现

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	knot[0]=0.0,knot[1]=0.0,knot[2]=0.0,knot[3]=0.0,knot[4]=0.5,knot[5]=0.5;//分段三次Bezier
	knot[6]=0.5,knot[7]=1.0,knot[8]=1.0,knot[9]=1.0,knot[10]=1.0;
	n=6,k=3;		
	P[0].x=-319,  P[0].y=-14;
	P[1].x=-269,  P[1].y=202;
	P[2].x= -61,  P[2].y=198;
	P[3].x= -32,  P[3].y=13;
	P[4].x= 54,   P[4].y=-116;
	P[5].x= 253,  P[5].y=-76;
	P[6].x= 296,  P[6].y=66;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);
	double tStep=0.01;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0.0,0.0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if (k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

在这里插入图片描述

2.5 非均匀B样条曲线

与其他类型的B样条曲线不同的是，给定控制点Pi, i = 0, 1,…, n，欲定义一条k次非均匀B样条曲线，还必须计算节点矢量 中具体的节点值。利用曲线的分段连接点与控制多边形的边对应关系，可以自动计算节点矢量。常用的算法有Hartley-Judd算法。

2.5.1 Hartley-Judd算法

1978年，Hartley和Judd认为应该根据曲线的连续性，分别考察每个控制多边形的k条边的和，然后再予以规范化。这就是Hartley-Judd算法。定义域内节点区间长度按下式计算：
在这里插入图片描述
在这里插入图片描述

2.5.2 代码实现

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	n=4; k=2;		
	P[0].x=-200,  P[0].y=100;
	P[1].x=-150,  P[1].y=-100;
	P[2].x=0,     P[2].y=250;
	P[3].x=150,   P[3].y=-100;
	P[4].x=200,   P[4].y=100;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	GetKnotVector();
	DrawBSplineCurve(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::GetKnotVector()// Hartley-Judd方法获取节点值
{
   for(int i=0;i<=k;i++) //小于次数k的节点值为0
      knot[i]=0.0;
   for(int i=n+1;i<=n+k+1;i++)//大于n的节点值为1
       knot[i]=1.0;
   //计算n-k个内节点
   for(int i=k+1;i<=n;i++)
   {
	   double sum=0.0;
	   for(int j=k+1;j<=i;j++)//公式（5-24）
	   { 
		   double numerator=0.0;//计算分子
		   for(int loop=j-k;loop<=j-1;loop++)
		   {
			   numerator+=sqrt((P[loop].x-P[loop-1].x)*(P[loop].x-P[loop-1].x)+(P[loop].y-P[loop-1].y)*(P[loop].y-P[loop-1].y));//计算两个点之间的距离
		   }
		   double denominator=0.0;//计算分母
		   for(int loop1=k+1;loop1<=n+1;loop1++)
		   {
			   for(int loop2=loop1-k;loop2<=loop1-1;loop2++)
			   {
				   denominator+=sqrt((P[loop2].x-P[loop2-1].x)*(P[loop2].x-P[loop2-1].x)+(P[loop2].y-P[loop2-1].y)*(P[loop2].y-P[loop2-1].y));//计算两个点之间的距离
				}
		   }	
		   sum+=numerator/denominator;//计算节点值
	   } 
       knot[i]=sum;
   }
}

void CGeometricfiguretestView::DrawBSplineCurve(CDC* pDC)//绘制B样条曲线
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,2,RGB(255,0,0));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);
	double tStep=0.01;
    for(double t=0.0;t<=1.0;t+=tStep)
	{	
		CP2 p(0.0,0.0);
	   	for(int i=0;i<=n;i++)
		{
			double BValue=BasisFunctionValue(t,i,k);			
			p+=P[i]*BValue;//B样条曲线定义
		}
		if(0.0==t)
			pDC->MoveTo(ROUND(p.x),ROUND(p.y));
		else
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}  
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	CBrush NewBrush,*pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0,0,0));
	pOldBrush=pDC->SelectObject(&NewBrush);
	for(int i=0;i<=n;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
	pDC->SelectObject(pOldPen);
}

double CGeometricfiguretestView::BasisFunctionValue(double t, int i, int k)//根据参数t值和次数k与节点矢量knot，计算第i个k次的B样条基函数
{
	double value1,value2,value;
	if(k==0)
	{
		if(t>=knot[i] && t<knot[i+1])
			return 1.0;
		else
			return 0.0;
	}
	if(k>0)
	{
		if(t<knot[i]||t>knot[i+k+1])
			return 0.0;
		else
		{
			double coffcient1,coffcient2;//凸组合系数1，凸组合系数2
			double denominator=0.0;//分母
			denominator=knot[i+k]-knot[i];//递推公式第一项分母
			if(denominator==0.0)//约定0/0
				coffcient1=0.0;
			else
				coffcient1=(t-knot[i])/denominator;
			denominator=knot[i+k+1]-knot[i+1];//递推公式第二项分母
			if(0.0==denominator)//约定0/0
				coffcient2=0.0;
			else
				coffcient2=(knot[i+k+1]-t)/denominator;
			value1=coffcient1*BasisFunctionValue(t,i,k-1);//递推公式第一项的值
			value2=coffcient2*BasisFunctionValue(t,i+1,k-1);//递推公式第二项的值
			value=value1+value2;//基函数的值
		}
	}
	return value;
}

在这里插入图片描述

© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
综合
# 计算几何
喜欢就支持一下吧
点赞201 分享
沉默的舞台剧的头像-卡核
计算几何03_三次参数样条曲线与Cardinal曲线-卡核
计算几何03_三次参数样条曲线与Cardinal曲线
计算几何03_三次参数样条曲线与Cardinal曲线
2年前 8870
计算几何07_NURBS曲线与曲面-卡核
计算几何07_NURBS曲线与曲面
计算几何07_NURBS曲线与曲面
2年前 8652
计算几何06_B样条曲面-卡核
计算几何06_B样条曲面
计算几何06_B样条曲面
2年前 7354
计算几何01_项目搭建与鼠标绘制直线-卡核
计算几何01_项目搭建与鼠标绘制直线
计算几何01_项目搭建与鼠标绘制直线
2年前 5270
计算几何02_三次样条曲线-卡核
计算几何02_三次样条曲线
计算几何02_三次样条曲线
2年前 5173
计算几何04_Bezier曲线与曲面-卡核
计算几何04_Bezier曲线与曲面
计算几何04_Bezier曲线与曲面
2年前 5030
相关推荐
卡核推荐优秀的开源工业软件内核源码 持续更新中-卡核
卡核推荐优秀的开源工业软件内核源码 持续更新中
卡核推荐优秀的开源工业软件内核源码 持续更新中
2年前 7.3W+
从三维工程软件正向设计谈起-卡核
从三维工程软件正向设计谈起
从三维工程软件正向设计谈起
3个月前 5.7W+
[转]我国CAD软件产业亟待研究现状采取对策-卡核
[转]我国CAD软件产业亟待研究现状采取对策
[转]我国CAD软件产业亟待研究现状采取对策
3个月前 5.5W+
Sweep折角过渡处理-卡核
Sweep折角过渡处理
Sweep折角过渡处理
12天前 4.8W+
BRepNet-基于AI的3D特征识别-卡核
BRepNet-基于AI的3D特征识别
BRepNet-基于AI的3D特征识别
3个月前 4.5W+
曲线积分量计算-卡核
曲线积分量计算
曲线积分量计算
3个月前 4.3W+
评论 抢沙发
头像
欢迎您留下宝贵的见解！
提交
头像

昵称

取消
昵称

请填写用户信息：

  • 昵称(必填)
  • 邮箱(必填)
表情
[aoman][baiyan][bishi][bizui][cahan][ciya][dabing][daku][deyi][doge][fadai][fanu][fendou][ganga][guzhang][haixiu][hanxiao][zuohengheng][zhuakuang][zhouma][zhemo][zhayanjian][zaijian][yun][youhengheng][yiwen][yinxian][xu][xieyanxiao][xiaoku][xiaojiujie][xia][wunai][wozuimei][weixiao][weiqu][tuosai][tu][touxiao][tiaopi][shui][se][saorao][qiudale][qinqin][qiaoda][piezui][penxue][nanguo][liulei][liuhan][lenghan][leiben][kun][kuaikule][ku][koubi][kelian][keai][jingya][jingxi][jingkong][jie][huaixiao][haqian][aini][OK][qiang][quantou][shengli][woshou][gouyin][baoquan][aixin][bangbangtang][xiaoyanger][xigua][hexie][pijiu][lanqiu][juhua][hecai][haobang][caidao][baojin][chi][dan][kulou][shuai][shouqiang][yangtuo][youling]
代码

请输入代码：

确认
图片

    暂无评论内容