计算几何04_Bezier曲线与曲面

0503047

在这里插入图片描述

一、Bezier曲线

1.1 Bezier曲线定义

给定n+1个控制点Pi（i＝0，1，2，…，n），则n次Bezier曲线定义为：
在这里插入图片描述
式中，t∈[0,1]，Pi（i＝0，1，2，…，n）是控制多边形的n+1个控制点。

Bi,n(t) 是Bernstein多项式，称为Bernstein基函数，其表达式为：
在这里插入图片描述
式中（i＝0，1，2，…，n）。

从式中可以看出：Bezier曲线是控制多边形的控制点关于Bernstein基函数的加权和。Bezier曲线的次数为n，则需要n+1个控制点来定义。在实际应用中，二次Bezier曲线缺乏应有的灵活性，三次Bezier曲线在工程领域应用较为广泛，高次Bezier曲线一般较少应用。

1.2 Bernstein基函数

1.2.1 定义

在这里插入图片描述

1.2.2 性质

1.2.2.1 正权性

在这里插入图片描述

1.2.2.2 基性

在这里插入图片描述

1.2.2.3 递推公式

在这里插入图片描述

1.2.2.4 端点插值性

在这里插入图片描述

1.2.2.5 导数

在这里插入图片描述

1.2.3 三次Bezier基函数算法代码实现

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;

	// TODO: add draw code for native data here
	CRect rect;
	GetClientRect(&rect);
	pDC->SetMapMode(MM_ANISOTROPIC);
	pDC->SetWindowExt(rect.Width(), rect.Height());
	pDC->SetViewportExt(rect.Width(), -rect.Height());
	pDC->SetViewportOrg(rect.Width()/6,rect.Height()*0.9);
	DrawUcs(pDC);
	DrawBasisFun03(pDC);
	DrawBasisFun13(pDC);
	DrawBasisFun23(pDC);
	DrawBasisFun33(pDC);
}

// 网格绘制
void CGeometricfiguretestView::DrawUcs(CDC *pDC)
{
	
	pDC->MoveTo(0,0);
	pDC->LineTo(0,300);
	pDC->MoveTo(0,0);
	pDC->LineTo(500,0);
	pDC->MoveTo(500,300);
	pDC->LineTo(0,300);
	pDC->MoveTo(500,300);
	pDC->LineTo(500,0);
	for(int m=50;m<=250;m=m+50)
	{
		
		for(int n=100;n<=500;n=n+100)
		{
			CPen NewPen,*pOldPen;
			NewPen.CreatePen(PS_DASH,1,RGB(0,0,0));
			pOldPen=pDC->SelectObject(&NewPen);
			pDC->MoveTo(0,m);
			pDC->LineTo(n,m);
			pDC->SelectObject(pOldPen);
		}
	}
		for(int a=100;a<=400;a=a+100)
	{
			
		for(int b=50;b<=300;b=b+50)
		{
			CPen NewPen,*pOldPen;
			NewPen.CreatePen(PS_DASH,1,RGB(0,0,0));
			pOldPen=pDC->SelectObject(&NewPen);
			pDC->MoveTo(a,0);
			pDC->LineTo(a,b);
			pDC->SelectObject(pOldPen);
		}

	}
}
void CGeometricfiguretestView::DrawBasisFun03(CDC *pDC)
{

	CPen NewPen1, *pOldPen;
	NewPen1.CreatePen(PS_SOLID,1,RGB(255,0,0));
	pOldPen=pDC->SelectObject(&NewPen1);
	
	ScaleX=500;
	ScaleY=300;
	for(double t=0;t<1;t+=0.01)
	{
		x=t*ScaleX;
		y=(-pow(t,3)+3*pow(t,2)-3*t+1)*ScaleY;
		if(t==0)
		{
			pDC->MoveTo(Round(x),Round(y));
		}
		else
		{
			pDC->LineTo(Round(x),Round(y));
		}
		
	}
	pDC->SelectObject(pOldPen);
	pDC->TextOut(-50, 300, L"B03(t)");
}
void CGeometricfiguretestView::DrawBasisFun13(CDC* pDC)
{

	CPen NewPen2, *pOldPen;
	NewPen2.CreatePen(PS_DASHDOT,1,RGB(0,255,0));
	pOldPen=pDC->SelectObject(&NewPen2);
	ScaleX=500;
	ScaleY=300;
	for(double t=0;t<1;t+=0.01)
	{
		x=t*ScaleX;
		y=(3*pow(t,3)-6*pow(t,2)+3*t)*ScaleY;
		if(t==0)
		{
			pDC->MoveTo(Round(x),Round(y));
		}
		else
		{
			pDC->LineTo(Round(x),Round(y));
		}

	}
	pDC->SelectObject(pOldPen);
	pDC->TextOut(140, 150, L"B13(t)");
}
void CGeometricfiguretestView::DrawBasisFun23(CDC *pDC)
{

	CPen NewPen3, *pOldPen;
	NewPen3.CreatePen(PS_DASH,1,RGB(0,0,255));
	pOldPen=pDC->SelectObject(&NewPen3);
	ScaleX=500;
	ScaleY=300;
	for(double t=0;t<1;t+=0.01)
	{
		x=t*ScaleX;
		y=(-3*pow(t,3)+3*pow(t,2))*ScaleY;
		if(t==0)
		{
			pDC->MoveTo(Round(x),Round(y));
		}
		else
		{
			pDC->LineTo(Round(x),Round(y));
		}

	}
	pDC->SelectObject(pOldPen);
	pDC->TextOut(330, 150, L"B23(t)");
}
void CGeometricfiguretestView::DrawBasisFun33(CDC *pDC)
{

	CPen NewPen4, *pOldPen;
	NewPen4.CreatePen(PS_DOT,1,RGB(0,255,255));
	pOldPen=pDC->SelectObject(&NewPen4);
	ScaleX=500;
	ScaleY=300;
	for(double t=0;t<1;t+=0.1)
	{
		x=t*ScaleX;
		y=(pow(t,3))*ScaleY;
		if(t==0)
		{
			pDC->MoveTo(Round(x),Round(y));
		}
		else
		{
			pDC->LineTo(Round(x),Round(y));
		}
	}
	pDC->SelectObject(pOldPen);
	pDC->TextOut(500, 300, L"B33(t)");
}

在这里插入图片描述
上边这4段曲线都是三次多项式，在整个区间[0,1]上都不为0。说明不能使用控制多边形对曲线的形状进行局部调整，如果改变某一控制点位置，整段曲线都将受到影响。一般将函数值不为0的区间叫做曲线的支撑区间。

1.3 Bezier曲线端点性质

在这里插入图片描述

1.4 Bezier曲线实现

1.4.1 一次Bezier曲线（Linear Curve）

当n＝1时，Bezier曲线有2个控制点P0和P1，Bezier曲线是一次多项式(t∈[0,1])。
在这里插入图片描述
写成矩阵形式为：
在这里插入图片描述
可以看出，一次Bezier曲线是连接起点P0和终点P1的一段直线。

1.4.2 二次Bezier曲线（Quadratic Curve）

当n＝2时，Bezier曲线有3个控制点P0、P1和P2，Bezier曲线是二次多项式(t∈[0,1])。
在这里插入图片描述
写成矩阵形式为:
在这里插入图片描述
二次Bezier曲线是一段起点在P0，终点在P2的抛物线。

1.4.2.1 代码实现

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	ctrP[0].x = 200, ctrP[0].y = 500;
	ctrP[1].x = 700, ctrP[1].y = 200;
	ctrP[2].x = 800, ctrP[2].y = 500;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc) return;
	CRect rect;
	GetClientRect(&rect);
	pDC->SetMapMode(MM_ANISOTROPIC);
	pDC->SetWindowExt(rect.Width(), rect.Height());
	pDC->SetViewportExt(rect.Width(), rect.Height());
	pDC->SetViewportOrg(rect.Width()/100, rect.Height()/100);
	// TODO: add draw code for native data here
	DrawPolygon(pDC);
	Bezier_2(pDC);
}

//控制边绘制
void CGeometricfiguretestView::DrawPolygon(CDC* pDC)
{
	CPen NewPen, *pOldPen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 0));
	pOldPen = pDC->SelectObject(&NewPen);
	CBrush NewBrush, *pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0, 0, 0));//控制点
	pOldBrush = pDC->SelectObject(&NewBrush);
	pDC->MoveTo(ctrP[0]);
	pDC->Ellipse(ctrP[0].x - 5, ctrP[0].y - 5, ctrP[0].x + 5, ctrP[0].y + 5);//绘制控制多边形顶点
	for (int i = 1;i < 3;i++)
	{
		pDC->LineTo(ctrP[i]);
		pDC->Ellipse(ctrP[i].x - 5, ctrP[i].y - 5, ctrP[i].x + 5, ctrP[i].y + 5);//绘制控制多边形顶点
	}
	pDC->SelectObject(pOldPen);
	pDC->SelectObject(pOldBrush);
}

//二次Bezier曲线绘制
void CGeometricfiguretestView::Bezier_2(CDC* pDC)
{
	CPen NewPen, *pOldPen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 255));
	pOldPen = pDC->SelectObject(&NewPen);
	pDC->MoveTo(ctrP[0]);
	double tSteP = 0.01;
	for (double t = 0.0;t <= 1.0;t += tSteP)
	{
		double x = 0, y = 0;
		x += (t*t - 2 * t + 1)*ctrP[0].x + (2 * t - 2 * t*t)*ctrP[1].x + t*t*ctrP[2].x;
		y += (t*t - 2 * t + 1)*ctrP[0].y + (2 * t - 2 * t*t)*ctrP[1].y + t*t*ctrP[2].y;
		pDC->LineTo(x, y);
	}
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

在这里插入图片描述

1.4.3 三次Bezier曲线（Cubic Curve）

当n＝3时，Bezier曲线有四个控制点P0、P1、P2和P3，Bezier曲线是三次多项式(t∈[0,1])。
在这里插入图片描述
写成矩阵形式为：
在这里插入图片描述
三次贝齐尔曲线是自由曲线。

1.4.3.1 代码实现

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	ctrP[0].x = 200, ctrP[0].y = 500;
	ctrP[1].x = 400, ctrP[1].y = 200;
	ctrP[2].x = 800, ctrP[2].y = 100;
	ctrP[3].x = 900, ctrP[3].y = 600;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;

	// TODO: add draw code for native data here
	DrawPolygon(pDC);
	Bezier_3(pDC);
}

void CGeometricfiguretestView::DrawPolygon(CDC* pDC)
{
	CPen NewPen, *pOldPen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 0));
	pOldPen = pDC->SelectObject(&NewPen);
	CBrush NewBrush, *pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0, 0, 0));//控制点颜色
	pOldBrush = pDC->SelectObject(&NewBrush);
	pDC->MoveTo(ctrP[0]);
	pDC->Ellipse(ctrP[0].x - 5, ctrP[0].y - 5, ctrP[0].x + 5, ctrP[0].y + 5);//绘制控制多边形顶点
	for (int i = 1;i < 4;i++)
	{
		pDC->LineTo(ctrP[i]);
		pDC->Ellipse(ctrP[i].x - 5, ctrP[i].y - 5, ctrP[i].x + 5, ctrP[i].y + 5);//绘制控制多边形顶点
	}
	pDC->SelectObject(pOldPen);
	pDC->SelectObject(pOldBrush);
}

void CGeometricfiguretestView::Bezier_3(CDC* pDC)
{
	CPen NewPen, *pOldPen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 255));
	pOldPen = pDC->SelectObject(&NewPen);
	pDC->MoveTo(ctrP[0]);
	double tSteP = 0.01;
	for (double t = 0.0;t <= 1.0;t += tSteP)
	{
		double x = 0, y = 0;
		x += (-t*t*t + 3 * t*t - 3 * t + 1)*ctrP[0].x + (3 * t*t*t - 6 * t*t + 3 * t)*ctrP[1].x + (-3 * t*t*t + 3 * t*t)*ctrP[2].x + (t*t*t)*ctrP[3].x;
		y += (-t*t*t + 3 * t*t - 3 * t + 1)*ctrP[0].y + (3 * t*t*t - 6 * t*t + 3 * t)*ctrP[1].y + (-3 * t*t*t + 3 * t*t)*ctrP[2].y + (t*t*t)*ctrP[3].y;
		pDC->LineTo(x, y);
	}
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

在这里插入图片描述

1.4.4 n次Bezier曲线

根据Bezier曲线定义，抽象出参数化n次Bezier曲线：

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	n=5;
	P[0].x=-500,P[0].y=-200;
	P[1].x=-300,P[1].y=100;
	P[2].x=100, P[2].y=200;
	P[3].x = 200, P[3].y = -200;
	P[4].x = 400, P[4].y = -100;
	P[5].x=600, P[5].y=200;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;
	GetClientRect(&rect);
	pDC->SetMapMode(MM_ANISOTROPIC);
	pDC->SetWindowExt(rect.Width(), rect.Height());
	pDC->SetViewportExt(rect.Width(), -rect.Height());
	pDC->SetViewportOrg(rect.Width() / 2,rect.Height() / 2);
	DrawBezier(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBezier(CDC* pDC)
{
	pDC->MoveTo(ROUND(P[0].x),ROUND(P[0].y));
	double tStep=0.01;//参数步长
	for (double t=0.0; t<=1.0; t+=tStep)
	{
		double x=0.0, y=0.0;
		for(int i=0;i<n+1;i++)
		{
			x+=P[i].x*Cni(n,i)*pow(t,i)*pow(1-t,n-i);//pow为幂函数
			y+=P[i].y*Cni(n,i)*pow(t,i)*pow(1-t,n-i);
		}
		pDC->LineTo(ROUND(x), ROUND(y));
	}
}
//组合数计算
double CGeometricfiguretestView::Cni(const int &n, const int &i)
{
	return double(Factorial(n))/(Factorial(i)*Factorial(n-i));
}
//阶乘计算
int CGeometricfiguretestView::Factorial(int n)
{
	int factorial;
	if(n==0||n==1)
		factorial=1;
	else
		factorial=n*Factorial(n-1);
	return factorial;
}

//绘制控制多边形
void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)
{
	for(int i=0;i<n+1;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x-5),ROUND(P[i].y)-5,ROUND(P[i].x+5),ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5, ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
}

在这里插入图片描述

二、Bezier曲线的de Casteljau算法

使用de Casteljau提出的递推算法，几何意义十分明显，可以直接进行做图。

2.1 de Casteljau递推公式

在这里插入图片描述

2.2 de Casteljau几何作图法

在这里插入图片描述

在这里插入图片描述

2.3 代码实现

CGeometricfiguretestView::CGeometricfiguretestView()
{
	// TODO: add construction code here
	n=3;
	P[0].x=-400,P[0].y=-200;
	P[1].x=-200,P[1].y=100;
	P[2].x=200, P[2].y=200;
	P[3].x=300, P[3].y=-200;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;
	GetClientRect(&rect);
	pDC->SetMapMode(MM_ANISOTROPIC);
	pDC->SetWindowExt(rect.Width(), rect.Height());
	pDC->SetViewportExt(rect.Width(), -rect.Height());
	pDC->SetViewportOrg(rect.Width() / 2,rect.Height() / 2);
	DrawBezier(pDC);
	DrawControlPolygon(pDC);
}

void CGeometricfiguretestView::DrawBezier(CDC* pDC)
{
	pDC->MoveTo(ROUND(P[0].x),ROUND(P[0].y));
	double tStep =0.01;//步长
	for (double t=0.0;t<=1.0;t+=tStep)
	{
		deCasteljau(t);
	    pDC->LineTo(ROUND(pp[0][n].x),ROUND(pp[0][n].y));
	}
}

void CGeometricfiguretestView::deCasteljau(double t) 
{
	for (int k=0;k<=n;k++)
	{
		pp[k][0].x=P[k].x;//将控制点一维数组赋给二维递归数组
		pp[k][0].y=P[k].y;
	}
	for (int r=1;r<=n;r++)//Casteljau递推公式,使用二维数组
		for(int i=0;i<=n-r;i++)
			pp[i][r]=(1-t)*pp[i][r-1]+t*pp[i+1][r-1];
}

//绘制控制多边形
void CGeometricfiguretestView::DrawControlPolygon(CDC* pDC)
{
	for(int i=0;i <n+1;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
}

在这里插入图片描述

三、Bezier曲线拼接

3.1 曲线拼接

Bezier曲线的次数随着控制多边形顶点数量的增加而增加。使用高次Bezier曲线计算起来代价很高，且容易有数值的舍入误差。而工程中常用的是三次Bezier曲线。为了描述复杂物体的轮廓曲线，经常需要将多段Bezier曲线拼接起来，并在结合处满足一定的连续性条件。

如下图，达到G1连续性的条件是: P2,P3 (Q0)和Q1三点共线,且P2和Q1位于拼接点P3 (Q0),的两侧。
在这里插入图片描述
从上图可以看出：达到G1连续的话需要有 （P3-P2）=a（Q1-Q0） 。

其中a是比例因子，其作用是控制拼接两端的长度比例，一般默认值为1。

3.2 代码实现

3.2.1 CCubicBezierCurve类封装

#pragma once
#include "P2.h"

class CCubicBezierCurve
{
public:
	CCubicBezierCurve(void);
	CCubicBezierCurve(CP2* P,int ptNum);
	~CCubicBezierCurve(void);
	void Draw(CDC* pDC);//绘制三次Bezier曲线
	void DrawControlPolygon(CDC* pDC);//绘制控制多边形
private:
	double Cni(const int &n,const int &i);//Bernstein第一项组合
	int Factorial(int n);//阶乘函数
private:
	CP2 P[4];//控制点数组
	int num;//曲线次数
};



#include "StdAfx.h"
#include "CubicBezierCurve.h"
#include <math.h>
#define  ROUND(d) int(d+0.5)

CCubicBezierCurve::CCubicBezierCurve(void)
{
}

CCubicBezierCurve::CCubicBezierCurve(CP2* P,int ptNum)
{
	for(int i=0;i< ptNum;i++)
		this->P[i]=P[i];
	num=ptNum-1;//曲线次数为控制点个数减一
}
CCubicBezierCurve::~CCubicBezierCurve(void)
{
}

void CCubicBezierCurve::Draw(CDC* pDC)
{
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,1,RGB(0,0,255));//曲线颜色为蓝色
	pOldPen = pDC->SelectObject(&NewPen);
	pDC->MoveTo(ROUND(P[0].x),ROUND(P[0].y));
	double tStep=0.01;//参数t的步长
	for (double t=0.0;t<=1.0;t+=tStep)
	{
		CP2 p(0.0,0.0);
		for (int i=0;i<=num;i++)
			p+=P[i]*Cni(num,i)*pow(t,i)*pow(1-t,num-i);
		pDC->LineTo(ROUND(p.x),ROUND(p.y));
	}
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

double CCubicBezierCurve::Cni(const int &n,const int &i)//Bernstein第一项组合
{
	return double(Factorial(n))/(Factorial(i)*Factorial(n-i));
}

int CCubicBezierCurve::Factorial(int n)//阶乘函数
{
	int factorial;
	if (n==0||n==1)
		factorial=1;
	else
		factorial=n*Factorial(n-1);
	return factorial;
}

void CCubicBezierCurve::DrawControlPolygon(CDC* pDC)//绘制控制多边形
{
	CBrush NewBrush,*pOldBrush;
	pOldBrush=(CBrush*)pDC->SelectStockObject(BLACK_BRUSH);//选择黑色库画刷
	for(int i=0;i<=num;i++)
	{
		if(0==i)
		{
			pDC->MoveTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);			
		}
		else
		{
			pDC->LineTo(ROUND(P[i].x),ROUND(P[i].y));
			pDC->Ellipse(ROUND(P[i].x)-5,ROUND(P[i].y)-5,ROUND(P[i].x)+5,ROUND(P[i].y)+5);
		}
	}
	pDC->SelectObject(pOldBrush);
}

3.2.2 代码实现

void CGeometricfiguretestView::ReadPoint()
{
	const double m = 0.5523;
	double r = 200;
	P[0].x = r,     P[0].y = 0.0;
	P[1].x = r,     P[1].y = m * r;
	P[2].x = m * r, P[2].y = r;
	P[3].x = 0,     P[3].y = r;
	P[4].x =-m * r, P[4].y = r;
	P[5].x =-r,     P[5].y = m * r;
	P[6].x =-r,     P[6].y = 0;
	P[7].x =-r,     P[7].y =-m * r;
	P[8].x =-m * r, P[8].y =-r;
	P[9].x = 0,     P[9].y =-r;
	P[10].x = m * r,P[10].y =-r;
	P[11].x = r,    P[11].y =-m * r;
}

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;
	GetClientRect(&rect);
	pDC->SetMapMode(MM_ANISOTROPIC);
	pDC->SetWindowExt(rect.Width(),rect.Height());
	pDC->SetViewportExt(rect.Width(),-rect.Height());
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);
	ReadPoint();
	p1[0] = P[0], p1[1] = P[1],  p1[2] = P[2],  p1[3] = P[3];
	p2[0] = P[3], p2[1] = P[4],  p2[2] = P[5],  p2[3] = P[6];
	p3[0] = P[6], p3[1] = P[7],  p3[2] = P[8],  p3[3] = P[9];
	p4[0] = P[9], p4[1] = P[10], p4[2] = P[11], p4[3] = P[0];
	CCubicBezierCurve Bezier1(p1,4);
	Bezier1.Draw(pDC);
	Bezier1.DrawControlPolygon(pDC);
	CCubicBezierCurve Bezier2(p2,4);
	Bezier2.Draw(pDC);
	Bezier2.DrawControlPolygon(pDC);
	CCubicBezierCurve Bezier3(p3,4);
	Bezier3.Draw(pDC);
	Bezier3.DrawControlPolygon(pDC);
	CCubicBezierCurve Bezier4(p4,4);
	Bezier4.Draw(pDC);
	Bezier4.DrawControlPolygon(pDC);
}

在这里插入图片描述

四、Bezier曲面

4.1 Bezier曲面定义

Bezier曲面由Bezier曲线拓广而来，它以两组正交的Bezier曲线控制点构造空间网格来，生成曲面. m x n次张量积形式的Bezier曲面的定义如下：
在这里插入图片描述
式中， （u，v）∈[0，1]×[0，1] , Pi,j = 0, 1,…, m,j=0, 1,…,n 是(m+ 1)x(n+1)个控制点。Bi,m(u)和Bj,n(v) 是Bernstein基函数。依次用线段连接点列 Pij， i= 0,1,…, m，j= 0, 1,…,n 中相邻两点所形成的空间网格称为控制网格。当m=3, n=3时, 由4×4=16个控制点构成控制网格，其相应的曲面称为双三次Bezier曲面片(Bicubic Bezier Patch)。

4.2 双三次Bezier曲面的定义

在这里插入图片描述
相应的曲面称为双三次Bezier曲面片（Bicubic Bezier Patch）。
展开上式，有：
在这里插入图片描述
式中，各项B#,#(#)为三次Bernstein基函数：
在这里插入图片描述
在这里插入图片描述
将上两个式子带入定义展开式中，有：
在这里插入图片描述
此时，令：
在这里插入图片描述
则有：
在这里插入图片描述
式中，Mbe 为对称矩阵。即，
在这里插入图片描述

生成曲面时，可以通过先固定u, 变化v得到一簇贝齐尔曲线；然后固定v，变化u得到另一簇贝齐尔曲线，两簇曲线交织生成双三次贝齐尔曲面。

4.3 代码实现

4.3.1 P3/BicubicBezierPatch类封装

为了实现曲面，我们需要拓充三维点类及曲面类，如下：
P3类：

#pragma once
#include "p2.h"
class CP3 :	public CP2
{
public:
	CP3(void);
	~CP3(void);
	CP3(double x ,double y,double z);
	friend CP3 operator +(const CP3 &p0, const CP3 &p1);//运算符重载
	friend CP3 operator -(const CP3 &p0, const CP3 &p1);
	friend CP3 operator *(const CP3 &p, double scalar);
	friend CP3 operator *(double scalar,const CP3 &p);
	friend CP3 operator /(const CP3 &p, double scalar);
public:
	double z;
};

#include "StdAfx.h"
#include "P3.h"
#include <math.h>

CP3::CP3(void)
{
	z=0.0;
}

CP3::~CP3(void)
{
}

CP3::CP3(double x,double y,double z):CP2(x,y)
{
	this->z=z;
}

CP3 operator +(const CP3 &p0, const CP3 &p1)//和
{	
	CP3 result;
	result.x = p0.x + p1.x;
	result.y = p0.y + p1.y;
	result.z = p0.z + p1.z;
	return result;
}

CP3 operator -(const CP3 &p0, const CP3 &p1)//差
{
	CP3 result;
	result.x = p0.x - p1.x;
	result.y = p0.y - p1.y;
	result.z = p0.z - p1.z;
	return result;
}

CP3 operator *(const CP3 &p, double scalar)//点和常量的积
{	
	return CP3(p.x * scalar, p.y * scalar, p.z * scalar);
}

CP3 operator *(double scalar, const CP3 &p)//点和常量的积
{	
	return CP3(p.x * scalar, p.y * scalar, p.z * scalar);
}

CP3 operator /(const CP3 &p, double scalar)//数除
{
	if(fabs(scalar)<1e-6)
		scalar = 1.0;
	CP3 result;
	result.x = p.x / scalar;
	result.y = p.y / scalar;
	result.z = p.z / scalar;
	return result;
}

BicubicBezierPatch类：

#pragma once
#include "P3.h"

class CBicubicBezierPatch
{
public:
	CBicubicBezierPatch(void);
	~CBicubicBezierPatch(void);
	void ReadControlPoint(CP3 P[4][4]);//读入16个控制点
	void DrawCurvedPatch(CDC* pDC);//绘制双三次Bezier曲面片
	void DrawControlGrid(CDC* pDC);//绘制控制网格
private:
	void LeftMultiplyMatrix(double M[][4],CP3 P[][4]);//左乘顶点矩阵
	void RightMultiplyMatrix(CP3 P[][4],double M[][4]);//右乘顶点矩阵
	void TransposeMatrix(double M[][4]);//转置矩阵
	CP2 ObliqueProjection(CP3 Point3);//斜二测投影
public:
	CP3 P[4][4];//三维控制点
};



#include "StdAfx.h"
#include "BicubicBezierPatch.h"
#include <math.h>
#define ROUND(d) int(d+0.5)

CBicubicBezierPatch::CBicubicBezierPatch(void)
{
}

CBicubicBezierPatch::~CBicubicBezierPatch(void)
{
}

void CBicubicBezierPatch::ReadControlPoint(CP3 P[4][4])
{
   for(int i=0;i<4;i++)
	   for(int j=0;j<4;j++)
   			this->P[i][j]=P[i][j];
}
void CBicubicBezierPatch::DrawCurvedPatch(CDC* pDC)
 {
	CPen NewPen, *pOldPen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(0, 0, 255));//曲线颜色为蓝色
	pOldPen = pDC->SelectObject(&NewPen);
	double M[4][4];//系数矩阵Mbe
	M[0][0]=-1;M[0][1]=3; M[0][2]=-3;M[0][3]=1;
	M[1][0]=3; M[1][1]=-6;M[1][2]=3; M[1][3]=0;
	M[2][0]=-3;M[2][1]=3; M[2][2]=0; M[2][3]=0;
	M[3][0]=1; M[3][1]=0; M[3][2]=0; M[3][3]=0;
	CP3 P3[4][4];//曲线计算用控制点数组
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			P3[i][j]=P[i][j];
	LeftMultiplyMatrix(M,P3);//数字矩阵左乘三维点矩阵
	TransposeMatrix(M);//计算转置矩阵
	RightMultiplyMatrix(P3,M);//数字矩阵右乘三维点矩阵
	double Step =0.1;//步长
	double u0,u1,u2,u3,v0,v1,v2,v3;//u，v参数的幂
	for(double u=0;u<=1;u+=Step)
		for(double v=0;v<=1;v+=Step)
		{
			u3=u*u*u,u2=u*u,u1=u,u0=1;
			v3=v*v*v,v2=v*v,v1=v,v0=1;
			CP3 pt=(u3*P3[0][0]+u2*P3[1][0]+u1*P3[2][0]+u0*P3[3][0])*v3
			          +(u3*P3[0][1]+u2*P3[1][1]+u1*P3[2][1]+u0*P3[3][1])*v2
			          +(u3*P3[0][2]+u2*P3[1][2]+u1*P3[2][2]+u0*P3[3][2])*v1
			          +(u3*P3[0][3]+u2*P3[1][3]+u1*P3[2][3]+u0*P3[3][3])*v0;
			CP2 Point2=ObliqueProjection(pt);//斜投影
			if(v==0)
				pDC->MoveTo(ROUND(Point2.x),ROUND(Point2.y));
			else
				pDC->LineTo(ROUND(Point2.x),ROUND(Point2.y));
		}		  
	for(double v=0;v<=1;v+=Step)
		for(double u=0;u<=1;u+=Step)
		{
			u3=u*u*u;u2=u*u;u1=u;u0=1;v3=v*v*v;v2=v*v;v1=v;v0=1;
			CP3 pt=(u3*P3[0][0]+u2*P3[1][0]+u1*P3[2][0]+u0*P3[3][0])*v3
			          +(u3*P3[0][1]+u2*P3[1][1]+u1*P3[2][1]+u0*P3[3][1])*v2
			          +(u3*P3[0][2]+u2*P3[1][2]+u1*P3[2][2]+u0*P3[3][2])*v1
			          +(u3*P3[0][3]+u2*P3[1][3]+u1*P3[2][3]+u0*P3[3][3])*v0;			
			CP2 Point2=ObliqueProjection(pt);//斜投影    
			if(0==u)
				pDC->MoveTo(ROUND(Point2.x),ROUND(Point2.y));
			else
				pDC->LineTo(ROUND(Point2.x),ROUND(Point2.y));
		}

	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

void CBicubicBezierPatch::LeftMultiplyMatrix(double M[][4],CP3 P[][4])//左乘矩阵M*P
{
	CP3 T[4][4];//临时矩阵
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			T[i][j]=M[i][0]*P[0][j]+M[i][1]*P[1][j]+M[i][2]*P[2][j]+M[i][3]*P[3][j];
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			P[i][j]=T[i][j];
}

void CBicubicBezierPatch::RightMultiplyMatrix(CP3 P[][4],double M[][4])//右乘矩阵P*M
{
	CP3 T[4][4];//临时矩阵
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			T[i][j]=P[i][0]*M[0][j]+P[i][1]*M[1][j]+P[i][2]*M[2][j]+P[i][3]*M[3][j];
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			P[i][j]=T[i][j];
}

void CBicubicBezierPatch::TransposeMatrix(double M[][4])//转置矩阵
{
	double T[4][4];//临时矩阵
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			T[j][i]=M[i][j];
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			M[i][j]=T[i][j];
}

CP2 CBicubicBezierPatch::ObliqueProjection(CP3 Point3)//斜二测投影
{
	CP2 Point2;
	Point2.x=Point3.x-Point3.z*sqrt(2.0)/2.0;
	Point2.y=Point3.y-Point3.z*sqrt(2.0)/2.0;
	return Point2;
}

void CBicubicBezierPatch::DrawControlGrid(CDC* pDC)//绘制控制网格
{
	CP2 P2[4][4];//二维控制点
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
			P2[i][j]=ObliqueProjection(P[i][j]);
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,3,RGB(0,0,0));
	pOldPen=pDC->SelectObject(&NewPen);
	for(int i=0;i<4;i++)
	{
		pDC->MoveTo(ROUND(P2[i][0].x),ROUND(P2[i][0].y));
		for(int j=1;j<4;j++)
			pDC->LineTo(ROUND(P2[i][j].x),ROUND(P2[i][j].y));
	}
	for(int j=0;j<4;j++)
	{
		pDC->MoveTo(ROUND(P2[0][j].x),ROUND(P2[0][j].y));
		for(int i=1;i<4;i++)
			pDC->LineTo(ROUND(P2[i][j].x),ROUND(P2[i][j].y));
	}
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
}

4.3.2 主函数调用

CP3 P[4][4];//控制点

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义客户区矩形
	GetClientRect(&rect);//获得客户区的大小
	pDC->SetMapMode(MM_ANISOTROPIC);//pDC自定义坐标系
	pDC->SetWindowExt(rect.Width(),rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(),-rect.Height());//设置视区范围,x轴水平向右，y轴垂直向上
	pDC->SetViewportOrg(rect.Width()/2,rect.Height()/2);//客户区中心为原点
	ReadPoint();
	DrawGraph(pDC);//绘制图形	
}

void CGeometricfiguretestView::ReadPoint()//读入控制多边形顶点
{
	P[0][0].x=20;  P[0][0].y=0;  P[0][0].z=200;
	P[0][1].x=0;   P[0][1].y=100;P[0][1].z=150;
	P[0][2].x=-130;P[0][2].y=100;P[0][2].z=50;
	P[0][3].x=-250;P[0][3].y=50; P[0][3].z=0;
	P[1][0].x=100; P[1][0].y=100;P[1][0].z=150;
	P[1][1].x= 30; P[1][1].y=100;P[1][1].z=100;
	P[1][2].x=-40; P[1][2].y=100;P[1][2].z=50;
	P[1][3].x=-110;P[1][3].y=100;P[1][3].z=0;
	P[2][0].x=280; P[2][0].y=90; P[2][0].z=140;
	P[2][1].x=110; P[2][1].y=120;P[2][1].z=80;
	P[2][2].x=0;   P[2][2].y=130;P[2][2].z=30;
	P[2][3].x=-100;P[2][3].y=150;P[2][3].z=-50;
	P[3][0].x=350; P[3][0].y=30; P[3][0].z=150;
	P[3][1].x=200; P[3][1].y=150;P[3][1].z=50;
	P[3][2].x=50;  P[3][2].y=200;P[3][2].z=0;
	P[3][3].x=0;   P[3][3].y=100;P[3][3].z =-70;
}

void CGeometricfiguretestView::DrawGraph(CDC* pDC)//绘制图形
{
	CBicubicBezierPatch patch;
	patch.ReadControlPoint(P);
	patch.DrawCurvedPatch(pDC);
	patch.DrawControlGrid(pDC);
}

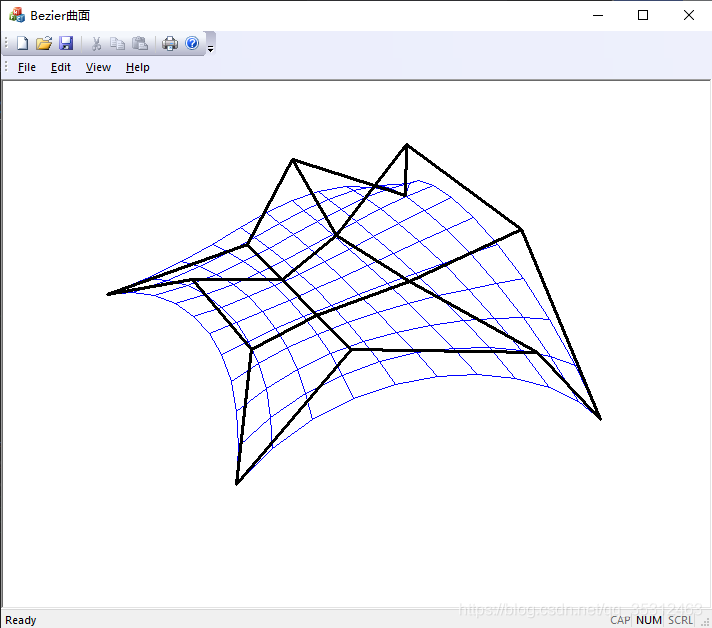
编译运行，如下：
在这里插入图片描述
我们也可以动态修改控制点，形成半桶面：

void CTestView::ReadPoint()//读入控制多边形顶点
{
	P[0][0].x = 20;  P[0][0].y = 0;  P[0][0].z = 200;
	P[0][1].x = 0;   P[0][1].y = 100; P[0][1].z = 150;
	P[0][2].x = -130; P[0][2].y = 100; P[0][2].z = 50;
	P[0][3].x = -250; P[0][3].y = 0; P[0][3].z = 0;
	P[1][0].x = 100; P[1][0].y = 0; P[1][0].z = 150;
	P[1][1].x = 30; P[1][1].y = 100; P[1][1].z = 100;
	P[1][2].x = -40; P[1][2].y = 100; P[1][2].z = 50;
	P[1][3].x = -110; P[1][3].y = 0; P[1][3].z = 0;
	P[2][0].x = 280; P[2][0].y = 0; P[2][0].z = 140;
	P[2][1].x = 110; P[2][1].y = 100; P[2][1].z = 80;
	P[2][2].x = 0;   P[2][2].y = 100; P[2][2].z = 30;
	P[2][3].x = -100; P[2][3].y = 0; P[2][3].z = -50;
	P[3][0].x = 350; P[3][0].y = 0; P[3][0].z = 150;
	P[3][1].x = 200; P[3][1].y = 100; P[3][1].z = 50;
	P[3][2].x = 50;  P[3][2].y = 100; P[3][2].z = 0;
	P[3][3].x = 0;   P[3][3].y = 0; P[3][3].z = -70;
}

在这里插入图片描述

© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
综合
# 计算几何
喜欢就支持一下吧
点赞47 分享
沉默的舞台剧的头像-卡核
计算几何03_三次参数样条曲线与Cardinal曲线-卡核
计算几何03_三次参数样条曲线与Cardinal曲线
计算几何03_三次参数样条曲线与Cardinal曲线
2年前 8870
计算几何07_NURBS曲线与曲面-卡核
计算几何07_NURBS曲线与曲面
计算几何07_NURBS曲线与曲面
2年前 8652
计算几何06_B样条曲面-卡核
计算几何06_B样条曲面
计算几何06_B样条曲面
2年前 7354
计算几何05_B样条曲线-卡核
计算几何05_B样条曲线
计算几何05_B样条曲线
2年前 5356
计算几何01_项目搭建与鼠标绘制直线-卡核
计算几何01_项目搭建与鼠标绘制直线
计算几何01_项目搭建与鼠标绘制直线
2年前 5270
计算几何02_三次样条曲线-卡核
计算几何02_三次样条曲线
计算几何02_三次样条曲线
2年前 5173
相关推荐
卡核推荐优秀的开源工业软件内核源码 持续更新中-卡核
卡核推荐优秀的开源工业软件内核源码 持续更新中
卡核推荐优秀的开源工业软件内核源码 持续更新中
2年前 7.3W+
从三维工程软件正向设计谈起-卡核
从三维工程软件正向设计谈起
从三维工程软件正向设计谈起
3个月前 5.7W+
[转]我国CAD软件产业亟待研究现状采取对策-卡核
[转]我国CAD软件产业亟待研究现状采取对策
[转]我国CAD软件产业亟待研究现状采取对策
3个月前 5.5W+
Sweep折角过渡处理-卡核
Sweep折角过渡处理
Sweep折角过渡处理
12天前 4.8W+
BRepNet-基于AI的3D特征识别-卡核
BRepNet-基于AI的3D特征识别
BRepNet-基于AI的3D特征识别
3个月前 4.5W+
曲线积分量计算-卡核
曲线积分量计算
曲线积分量计算
3个月前 4.3W+
评论 抢沙发
头像
欢迎您留下宝贵的见解！
提交
头像

昵称

取消
昵称

请填写用户信息：

  • 昵称(必填)
  • 邮箱(必填)
表情
[aoman][baiyan][bishi][bizui][cahan][ciya][dabing][daku][deyi][doge][fadai][fanu][fendou][ganga][guzhang][haixiu][hanxiao][zuohengheng][zhuakuang][zhouma][zhemo][zhayanjian][zaijian][yun][youhengheng][yiwen][yinxian][xu][xieyanxiao][xiaoku][xiaojiujie][xia][wunai][wozuimei][weixiao][weiqu][tuosai][tu][touxiao][tiaopi][shui][se][saorao][qiudale][qinqin][qiaoda][piezui][penxue][nanguo][liulei][liuhan][lenghan][leiben][kun][kuaikule][ku][koubi][kelian][keai][jingya][jingxi][jingkong][jie][huaixiao][haqian][aini][OK][qiang][quantou][shengli][woshou][gouyin][baoquan][aixin][bangbangtang][xiaoyanger][xigua][hexie][pijiu][lanqiu][juhua][hecai][haobang][caidao][baojin][chi][dan][kulou][shuai][shouqiang][yangtuo][youling]
代码

请输入代码：

确认
图片

    暂无评论内容