深入理解数值计算网格(6)–理解高阶网格

“由于高阶数值计算复杂性，目前大部分商业软件网格都是线性单元（0阶）或者二次单元（一阶）。实际上高阶网格（也就是常说的P单元）在处理复杂几何上更具优势，适当的设置网格参数，只需更少数量的网格，无需迭代，就能获得更好的数值计算解，期待未来在高阶领域有更多实际应用。”       

—-仿真软件十年回顾和展望(整理版)

关于高阶单元，之前的文章有过很多介绍。当网格密度偏小，计算精度不够的时，可以通过两种方法提高精度，一种是加密网格（h单元方法），另一种是提升网格的阶次(p单元)，不再多描述。

下面主要介绍高阶单元的一些特点和实现

1.单元划分和生成

0阶单元，1阶单元的网格几何信息并没有改变，也就是说原来的点，边，面的位置没有发生改变。区别在于高阶单元的边或者面上点的增加。

对于网格划分来讲，难度并没有变化，区别只是在已有单元的边上再加点。如果单元编号约定规则，把线性单元变成高阶单元在求解器阶段进行也可以。但考虑到模块解耦和功能独立性，一般还是把高阶网格的创建放在网格生成阶段。

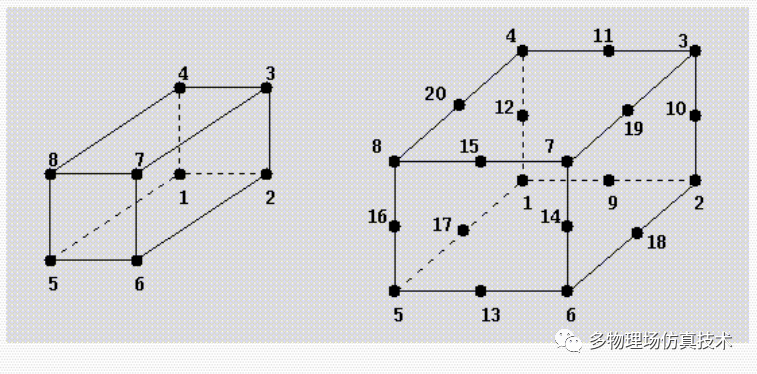
  左为线性六面体单元，右为曲线六面体单元

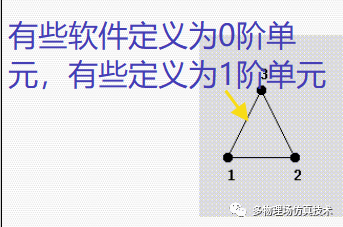
在实际应用中，发现有些软件将线性单元（即三角形单元中仅有三个顶点）描述为1阶单元，有些描述为0阶单位，在沟通中造成了歧义。

为了避免歧义，统一将顶点仅在边两端的单元（三角形三个顶点）称为线性单元，将边中间有点的单元称为曲线单元。

2. 高阶单元计算精度和计算资源

高阶单元之所以能提高精度，简单理解就是高阶单元使用的多项式变量次数更高，表达式更丰富，有能力更精准的反应单元内部物理量的变化。

大部分物理场的本构方程为二阶偏微分方程，或者可以转为二阶偏微分方程。高阶单元的基函数和形函数偏导后仍然能保证单元内部的非线性！

精度的提高的代价是计算量的快速增加，尤其是矩阵规模的增加

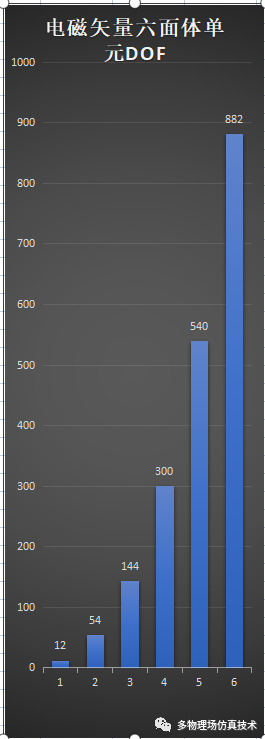
电磁六面体单元自由度数目随阶数变化

3.高阶单元实现

高阶单元实现有两种，一种是直接使用点插值的基函数方法，另一种是使用结构化组合基函数。

两种方法都基于线性单元，区别点在于第一种方法由单元上的一系列点来定义，高阶单元由增加插值点构成，因此在各个维度都有较好的独立性，且生成的刚度矩阵在预条件处理上有优势。多项式的每个表达式的系数有较好的物理含义，并且在边界上有较好的表达。不同阶数的单元有相同的统一表达式，代码更方便实现。

结构化组合基函数是由在低阶基函数的基础上乘以或加上新的函数。这样做的好处是在同一模型中可以使用不同阶的基函数，实现上灵活，但也增加了复杂度。

在实际研发中，更多的是采用第一种方法插值基函数的高阶单元。

混合单元

有限元等数值方法是在全局进行计算，所以可以在网格不容易生成的地方采用高阶单元，其它地方使用低阶一般单元，发挥各自的优点。

大部分有限元软件都支持高阶单元，在工程应用中，碰到网格划分困难，网格质量差，使用低阶单元收敛困难，且计算资源没有瓶颈的情况下可以尝试使用高阶单元。