第三十四讲:左右逆和伪逆
前面我们涉及到的逆(inverse)都是指左、右乘均成立的逆矩阵,即
A−1A=I=AA−1
A^{-1}A=I=AA^{-1}。在这种情况下,
m×n
m\\times n矩阵
A
A满足m=n=rank(A)m=n=rank(A),也就是满秩方阵。
左逆(left inserve)
记得我们在最小二乘一讲(第十六讲)介绍过列满秩的情况,也就是列向量线性无关,但行向量通常不是线性无关的。常见的列满秩矩阵
A
A满足m=n=rank(A)m=n=rank(A)(
情况1
\\color{red}{情况1})。
列满秩时,列向量线性无关,所以其
零空间
\\color{red}{零空间}中只有零解,方程
Ax=b
Ax=b可能有一个唯一解(
b
b在AA的列空间中,此特解就是全部解,因为通常的特解可以通过零空间中的向量扩展出一组解集,而此时零空间只有列向量),也可能无解(
b
b不在AA的列空间中)。
另外,此时行空间为
Rn
\\mathbb{R}^n,也正印证了与行空间互为正交补的零空间中只有列向量。
现在来观察
ATA
A^TA,也就是在
m>n=rank(A)
m>n=rank(A)(
情况2
\\color{red}{情况2})的情况下,
n×m
n\\times m矩阵乘以
m×n
m\\times n矩阵,结果为一个满秩的
n×n
n\\times n矩阵,所以
ATA
A^TA是一个可逆矩阵。也就是说
(ATA)−1ATA=I
\\underbrace{\\left(A^TA\\right)^{-1}A^T}A=I成立,而大括号部分的
(ATA)−1AT
\\left(A^TA\\right)^{-1}A^T称为长方形矩阵
A
A的左逆
A^{-1}_{left}=\\left(A^TA\\right)^{-1}A^T
- 顺便复习一下最小二乘一讲,通过关键方程
ATAx^=ATb
A^TA\\hat x=A^Tb,
A−1left
A^{-1}_{left}被当做一个系数矩阵乘在
b
b向量上,求得bb向量投影在
A
A的列空间之后的解x^=(ATA)−1ATb\\hat
x=\\left(A^TA\\right)^{-1}A^Tb。- 如果我们强行给左逆左乘矩阵
A
A,得到的矩阵就是投影矩阵P=A(ATA)−1ATP=A\\left(A^TA\\right)^{-1}A^T,来自
p=Ax^=A(ATA)−1AT
p=A\\hat
x=A\\left(A^TA\\right)^{-1}A^T,它将右乘的向量b
b投影在矩阵AA的列空间中。
再来观察
AAT
AA^T矩阵,这是一个
m×m
m\\times m矩阵,秩为
rank(AAT)=n<m
rank(AA^T)=n<m,也就是说
AAT
AA^T是不可逆的,那么接下来我们看看右逆。
2.右逆(right inverse)
可以与左逆对称的看,右逆也就是研究
m×n
m\\times n矩阵
A
A行满秩的情况,此时n>m=rank(A)n>m=rank(A)。对称的,其
左零空间
\\color{red}{左零空间}中仅有零向量,即没有行向量的线性组合能够得到零向量。
行满秩时,矩阵的列空间将充满向量空间
C(A)=Rm
C(A)=\\mathbb{R}^m,所以方程
Ax=b
Ax=b总是有解集,由于消元后有
n−m
n-m个自由变量,所以方程的零空间为
n−m
n-m维。
与左逆对称,再来观察
AAT
AA^T,在
n>m=rank(A)
n>m=rank(A)(
情况3
\\color{red}{情况3})的情况下,
m×n
m\\times n矩阵乘以
n×m
n\\times m矩阵,结果为一个满秩的
m×m
m\\times m矩阵,所以此时
AAT
AA^T是一个满秩矩阵,也就是
AAT
AA^T可逆。所以
AAT(AAT)=I
A\\underbrace{A^T\\left(AA^T\\right)}=I,大括号部分的
AT(AAT)
A^T\\left(AA^T\\right)称为长方形矩阵的右逆
A−1right=AT(AAT)
A^{-1}_{right}=A^T\\left(AA^T\\right)
同样的,如果我们强行给右逆右乘矩阵
A
A,将得到另一个投影矩阵P=AT(AAT)AP=A^T\\left(AA^T\\right)A,与上一个投影矩阵不同的是,这个矩阵的
A
A全部变为ATA^T了。所以这是一个能够将右乘的向量
b
b投影在AA的行空间中。
前面我们提及了逆(方阵满秩),并讨论了左逆(矩阵列满秩)、右逆(矩阵行满秩),现在看一下第四种情况,
m×n
m\\times n矩阵
A
A不满秩的情况。
3.伪逆(pseudo inverse)
3.1定义
有m×nm\\times n矩阵
A
A,满足rank(A)<min(m, n)rank(A)\\lt min(m,\\ n)(
情况4
\\color{red}{情况4}),则
-
列空间
C(A)∈Rm, dimC(A)=r
C(A)\\in\\mathbb{R}^m,\\ \\dim C(A)=r,左零空间N(AT)∈Rm, dimN(AT)=m−r
N\\left(A^T\\right)\\in\\mathbb{R}^m,\\ \\dim N\\left(A^T\\right)=m-r,列空间与左零空间互为正交补; -
行空间
C(AT)∈Rn, dimC(AT)=r
C\\left(A^T\\right)\\in\\mathbb{R}^n,\\ \\dim C\\left(A^T\\right)=r,零空间N(A)∈Rn, dimN(A)=n−r
N(A)\\in\\mathbb{R}^n,\\ \\dim N(A)=n-r,行空间与零空间互为正交补。
现在任取一个向量
x
x,乘上AA后结果
Ax
Ax一定落在矩阵
A
A的列空间C(A)C(A)中。而根据维数,
x∈Rn, Ax∈Rm
x\\in\\mathbb{R}^n,\\ Ax\\in\\mathbb{R}^m,那么我们现在猜测,输入向量
x
x全部来自矩阵的行空间,而输出向量AxAx全部来自矩阵的列空间,并且是一一对应的关系,也就是
Rn
\\mathbb{R}^n的
r
r维子空间到Rm\\mathbb{R}^m的
r
r维子空间的映射。
而矩阵AA现在有这些零空间存在,其作用是将某些向量变为零向量,这样
Rn
\\mathbb{R}^n空间的所有向量都包含在行空间与零空间中,所有向量都能由行空间的分量和零空间的分量构成,变换将零空间的分量消除。但如果我们只看行空间中的向量,那就全部变换到列空间中了。
那么,我们现在只看行空间与列空间,在行空间中任取两个向量
x, y∈C(AT)
x,\\ y\\in C(A^T),则有
Ax≠Ay
Ax\\neq Ay。所以从行空间到列空间,变换
A
A是个不错的映射,如果限制在这两个空间上,AA可以说“是个可逆矩阵”,那么它的逆就称作伪逆,而这个伪逆的作用就是将列空间的向量一一映射到行空间中。通常,伪逆记作
A+
A^+,因此
Ax=(Ax), y=A+(Ay)
Ax=(Ax),\\ y=A^+(Ay)。
现在我们来证明对于
x,y∈C(AT), x≠y
x,y\\in C\\left(A^T\\right),\\ x\\neq y,有
Ax,Ay∈C(A), Ax≠Ay
Ax,Ay\\in C(A),\\ Ax\\neq Ay:
- 反证法,设
Ax=Ay
Ax=Ay,则有
A(x−y)=0
A(x-y)=0,即向量
x−y∈N(A)
x-y\\in N(A);
-
另一方面,向量
x,y∈C(AT)
x,y\\in C\\left(A^T\\right),所以两者之差x−y
x-y向量也在C(AT)
C\\left(A^T\\right)中,即x−y∈C(AT)
x-y\\in C\\left(A^T\\right); -
此时满足这两个结论要求的仅有一个向量,即零向量同时属于这两个正交的向量空间,从而得到
x=y
x=y,与题设中的条件矛盾,得证。
伪逆在统计学中非常有用,以前我们做最小二乘需要矩阵列满秩这一条件,只有矩阵列满秩才能保证
ATA
A^TA是可逆矩阵,而统计中经常出现重复测试,会导致列向量线性相关,在这种情况下ATA
A^TA就成了奇异矩阵,这时候就需要伪逆。
3.2 伪逆求解
接下来我们介绍如何计算伪逆
A+
A^+:
- 其中一种方法是使用奇异值分解,
A=UΣVT
A=U\\varSigma V^T,其中的对角矩阵型为
Σ=⎡⎣⎢⎢⎢⎢⎢⎢σ1⋱σ2[0]⎤⎦⎥⎥⎥⎥⎥⎥
\\varSigma=\\left[\\begin{array}{c c c|c}\\sigma_1&&&\\\\&\\ddots&&\\\\&&\\sigma_2&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right],对角线非零的部分来自
ATA, AAT
A^TA,\\ AA^T比较好的部分,剩下的来自左/零空间。
我们先来看一下
Σ
\\varSigma矩阵的伪逆是多少,这是一个
m×n
m\\times n矩阵,
rank(Σ)=r
rank(\\varSigma)=r,
Σ+=⎡⎣⎢⎢⎢⎢⎢⎢⎢1σ1⋱1σr[0]⎤⎦⎥⎥⎥⎥⎥⎥⎥
\\varSigma^+=\\left[\\begin{array}{c c c|c}\\frac{1}{\\sigma_1}&&&\\\\&\\ddots&&\\\\&&\\frac{1}{\\sigma_r}&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right],伪逆与原矩阵有个小区别:这是一个
n×m
n\\times m矩阵。则有
ΣΣ+=⎡⎣⎢⎢⎢⎢⎢⎢1⋱1[0]⎤⎦⎥⎥⎥⎥⎥⎥m×m
\\varSigma\\varSigma^+=\\left[\\begin{array}{c c c|c}1&&&\\\\&\\ddots&&\\\\&&1&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]_{m\\times m},
Σ+Σ=⎡⎣⎢⎢⎢⎢⎢⎢1⋱1[0]⎤⎦⎥⎥⎥⎥⎥⎥n×n
\\varSigma^+\\varSigma=\\left[\\begin{array}{c c c|c}1&&&\\\\&\\ddots&&\\\\&&1&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]_{n\\times n}。
观察
ΣΣ+
\\varSigma\\varSigma^+和
Σ+Σ
\\varSigma^+\\varSigma不难发现,
ΣΣ+
\\varSigma\\varSigma^+是将向量投影到列空间上的投影矩阵,而
Σ+Σ
\\varSigma^+\\varSigma是将向量投影到行空间上的投影矩阵。我们不论是左乘还是右乘伪逆,得到的不是单位矩阵,而是投影矩阵,该投影将向量带入比较好的空间(行空间和列空间,而不是左/零空间)。
- 接下来我们来求
A
A的伪逆:
A+=VΣ+UTA^+=V\\varSigma^+U^T
4. 总结
1.
A是m×n
A是m×n,
m
m 行 nn 列
1)矩阵可逆:
即两边逆,
AA−1=I=A−1A
AA^{ -1} = I = A ^{-1} A ,此时
r=m=n
r=m=n,
A
A 为方阵且满秩,零空间和左零空间都只有零
向量。
2)左逆(m>n=rank(A)m>n=rank(A)):
当列满秩,列向量线性无关,行向量不一定,
r=n
r=n,零空间只有零向量,
Ax=b
Ax=b 存在 0 个或 1 个解。
ATA
A ^T A 是
n×n
n×n 的对称矩阵,满秩,
ATA
A ^T A 是可逆的,称
(ATA)−1AT
(A ^T A) ^{-1} A ^T 为
A
A 的左逆,因为(ATA)−1AT∗A=I(A T A)^{ -1} A ^T *A=I。这在最小二乘中至关重要,因为最小二乘以
ATA
A ^T A 为系数矩阵(为什么统计学家喜欢这些?因为统计学家最喜欢用最小二乘),在列满秩的情况下,
ATA
A ^T A 可逆。此时
[(ATA)−1AT]
[ (A ^T A) ^{-1} A ^T ]为
n×m
n×m,
A为m×n
A为m×n,得
I
I 为
n×n
n×n。
3)右逆(
n>m=rank(A)
n>m=rank(A)):
当行满秩,行向量线性无关,
r=m
r=m,
AT
A^ T 的零空间只含零向量,
Ax=b
Ax=b 有或无穷多个解,因为
A∗AT(AAT)−1=I
A*A^ T (AA ^T ) ^{-1} =I,所以把
AT(AAT)−1
A ^T (AA ^T ) ^{-1} 称为 A 的右逆。
4)伪逆(
rank(A)<min(m, n)
rank(A)\\lt min(m,\\ n)):
r<m,r<n
r<m,r<n,行空间和列空间的维数相同,都是
r
r 维,行空间的任意向量
x
x,与 AA 相乘,得到恰好是列空间中的所有向量,行空间向量
x
x 与列空间向量
Ax
Ax 的关系是一 一对应的。所有向量都能由行空间的分量和零空间的分量构成。
行空间中向量
x
x 对应着列空间中的 AxAx(零空间中的x
x 乘以A
A 得零 Ax=0Ax=0), 行空间中向量y
y 对应着列空间中的 AyAy。但如果要从列空间得到行空间的向量呢,要得到行空间的向量,那么
x=A+(Ax)
x=A ^+ (Ax),A+
A ^+ 就是伪逆,伪逆把左零空间变为0
0,即如果 A+A^+ 乘以左零空间的向量,结果为0
0。假设没有零空间的干扰,即假设零空间只有零向量,存在逆,那么行空间的向量x x 得到列空间的向量
Ax
Ax,反过来,通过A
A 的逆就能从列空间得到行空间, A−1(Ax)=xA ^{-1} (Ax)=x。
(ATA)−1AT∗A=I
(A ^T A) ^{-1} A^ T *A=I, 如果将左逆写在右边将得不到单位矩阵了, 那么A(ATA)−1AT
A(A ^T A) ^{-1} A ^T 是在列空间投影的投影矩阵,它会尽量靠近单位矩阵,一个投影矩阵很想成为单位矩阵,但不可能做到。
2.求解伪逆(SVD分解)
第三十五讲:期末复习
依然是从以往的试题入手复习知识点。
1.
已知
m×n
m\\times n矩阵
A
A,有Ax=⎡⎣⎢100⎤⎦⎥Ax=\\begin{bmatrix}1\\\\0\\\\0\\end{bmatrix}无解;
Ax=⎡⎣⎢010⎤⎦⎥
Ax=\\begin{bmatrix}0\\\\1\\\\0\\end{bmatrix}仅有唯一解,求关于
m,n,rank(A)
m,n,rank(A)的信息。
首先,最容易判断的是
m=3
m=3;而根据第一个条件可知,矩阵不满秩,有
r<m
r<m;根据第二个条件可知,零空间仅有零向量,也就是矩阵消元后没有自由变量,列向量线性无关,所以有
r=n
r=n。
综上,有
m=3>n=r
m=3>n=r。
根据所求写出一个矩阵
A
A的特例:A=⎡⎣⎢010001⎤⎦⎥A=\\begin{bmatrix}0& 0\\\\1& 0\\\\0& 1\\end{bmatrix}。
detATA=?detAAT
\\det A^TA\\stackrel{?}{=}\\det AA^T:不相等,因为
ATA
A^TA可逆而
AAT
AA^T不可逆,所以行列式不相等。(但是对于方阵,
detAB=detBA
\\det AB=\\det BA恒成立。)
-
ATA
A^TA可逆吗?是,因为r=n
r=n,矩阵列向量线性无关,即列满秩。 -
AAT
AA^T正定吗?否,因为AAT
AA^T是3×n
3\\times n矩阵与n×3
n\\times 3矩阵之积,是一个三阶方阵,而AAT
AA^T秩为2
2,所以不是正定矩阵。(不过AATAA^T一定是半正定矩阵。)求证
ATy=c
A^Ty=c至少有一个解:因为A
A的列向量线性无关,所以ATA^T的行向量线性无关,消元后每行都有主元,且总有自由变量,所以零空间中有非零向量,零空间维数是m−r
m-r(可以直接从dimN(AT)=m−r
\\dim N\\left(A^T\\right)=m-r得到结论)。
2.
设
A=[v1 v2 v3]
A=\\Bigg[v_1\\ v_2\\ v_3\\Bigg],对于
Ax=v1−v2+v3
Ax=v_1-v_2+v_3,求
x
x。
按列计算矩阵相乘,有x=⎡⎣⎢1−11⎤⎦⎥x=\\begin{bmatrix}1\\\\-1\\\\1\\end{bmatrix}。
-
若
Ax=v1−v2+v3=0
Ax=v_1-v_2+v_3=0,则解是唯一的吗?为什么。如果解释唯一的,则零空间中只有零向量,而在此例中x=⎡⎣⎢1−11⎤⎦⎥
x=\\begin{bmatrix}1\\\\-1\\\\1\\end{bmatrix}就在零空间中,所以解不唯一。 -
若
v1,v2,v3
v_1,v_2,v_3是标准正交向量,那么怎样的线性组合c1v1+c2v2
c_1v_1+c_2v_2能够最接近v3
v_3?此问是考察投影概念,由于是正交向量,所以只有0
0向量最接近v3v_3。
3.
矩阵
A=⎡⎣⎢.2.4.4.4.2.4.3.3.4⎤⎦⎥
A=\\begin{bmatrix}.2& .4& .3\\\\.4& .2& .3\\\\.4& .4& .4\\end{bmatrix},求稳态。
这是个马尔科夫矩阵,前两之和为第三列的两倍,奇异矩阵总有一个特征值为
0
0,而马尔科夫矩阵总有一个特征值为11,剩下一个特征值从矩阵的迹得知为
−.2
-.2。
再看马尔科夫过程,设从
u(0)
u(0)开始,
uk=Aku0,u0=⎡⎣⎢0100⎤⎦⎥
u_k=A^ku_0, u_0=\\begin{bmatrix}0\\\\10\\\\0\\end{bmatrix}。先代入特征值
λ1=0, λ2=1, λ3=−.2
\\lambda_1=0,\\ \\lambda_2=1,\\ \\lambda_3=-.2查看稳态
uk=c1λk1x1+c2λk2x2+c3λk3x3
u_k=c_1\\lambda_1^kx_1+c_2\\lambda_2^kx_2+c_3\\lambda_3^kx_3,当
k→∞
k\\to\\infty,第一项与第三项都会消失,剩下
u∞=c2x2
u_\\infty=c_2x_2。
到这里我们只需求出
λ2
\\lambda_2对应的特征向量即可,带入特征值求解
(A−I)x=0
(A-I)x=0,有
⎡⎣⎢−.8.4.4.4−.8.4.3.3−.6⎤⎦⎥⎡⎣⎢???⎤⎦⎥=⎡⎣⎢000⎤⎦⎥
\\begin{bmatrix}-.8& .4& .3\\\\.4& -.8& .3\\\\.4& .4& -.6\\end{bmatrix}\\begin{bmatrix}?\\\\?\\\\?\\end{bmatrix}=\\begin{bmatrix}0\\\\0\\\\0\\end{bmatrix},可以消元得,也可以直接观察得到
x2=⎡⎣⎢334⎤⎦⎥
x_2=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix}。
剩下就是求
c2
c_2了,可以通过
u0
u_0一一解出每个系数,但是这就需要解出每一个特征值。另一种方法,我们可以通过马尔科夫矩阵的特性知道,对于马尔科夫过程的每一个
uk
u_k都有其分量之和与初始值分量之和相等,所以对于
x2=⎡⎣⎢334⎤⎦⎥
x_2=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix},有
c2=1
c_2=1。所以最终结果是
u∞=⎡⎣⎢334⎤⎦⎥
u_\\infty=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix}。
4.
对于二阶方阵,回答以下问题:
求投影在直线
a=[4−3]
a=\\begin{bmatrix}4\\\\-3\\end{bmatrix}上的投影矩阵:应为
P=aaTaTa
P=\\frac{aa^T}{a^Ta}。
已知特征值
λ1=2, x1=[12]λ2=3, x2=[21]
\\lambda_1=2,\\ x_1=\\begin{bmatrix}1\\\\2\\end{bmatrix}\\quad \\lambda_2=3,\\ x_2=\\begin{bmatrix}2\\\\1\\end{bmatrix}求原矩阵
A
A:从对角化公式得A=SΛS−1=[1221][0003][1221]−1A=S\\Lambda S^{-1}=\\begin{bmatrix}1& 2\\\\2& 1\\end{bmatrix}\\begin{bmatrix}0& 0\\\\0& 3\\end{bmatrix}\\begin{bmatrix}1& 2\\\\2& 1\\end{bmatrix}^{-1},解之即可。
A
A是一个实矩阵,且对任意矩阵BB,
A
A都不能分解成A=BTBA=B^TB,给出
A
A的一个例子:我们知道BTBB^TB是对称的,所以给出一个非对称矩阵即可。 矩阵
A
A有正交的特征向量,但不是对称的,给出一个AA的例子:我们在三十三讲提到过,反对称矩阵,因为满足
AAT=ATA
AA^T=A^TA而同样具有正交的特征向量,所以有
A=[0−110]
A=\\begin{bmatrix}0& 1\\\\-1& 0\\end{bmatrix}或旋转矩阵
[cosθsinθ−sinθcosθ]
\\begin{bmatrix}\\cos\\theta& -\\sin\\theta\\\\\\sin\\theta& \\cos\\theta\\end{bmatrix},这些矩阵都具有复数域上的正交特征向量组。
5.最小二乘问题,因为时间的关系直接写出计算式和答案,
⎡⎣⎢111012⎤⎦⎥[CD]=⎡⎣⎢341⎤⎦⎥(Ax=b)
\\begin{bmatrix}1& 0\\\\1& 1\\\\1& 2\\end{bmatrix}\\begin{bmatrix}C\\\\D\\end{bmatrix}=\\begin{bmatrix}3\\\\4\\\\1\\end{bmatrix}(Ax=b),解得
[C^D^]=[113−1]
\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}=\\begin{bmatrix}\\frac{11}{3}\\\\-1\\end{bmatrix}。
求投影后的向量
p
p:向量pp就是向量
b
b在矩阵AA列空间中的投影,所以
p=⎡⎣⎢p1p2p3⎤⎦⎥=⎡⎣⎢111012⎤⎦⎥[C^D^]
p=\\begin{bmatrix}p_1\\\\p_2\\\\p_3\\end{bmatrix}=\\begin{bmatrix}1& 0\\\\1& 1\\\\1& 2\\end{bmatrix}\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}。
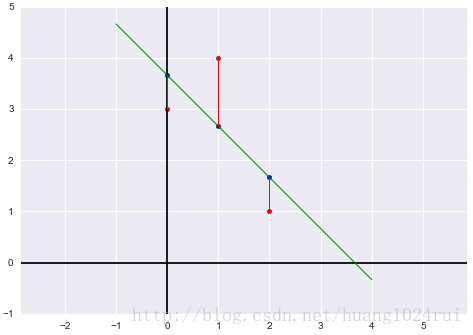
求拟合直线的图像:
x=0,1,2
x=0,1,2时
y=p1,p2,p2
y=p_1,p_2,p_2所在的直线的图像,
y=C^+D^x
y=\\hat C+\\hat Dx即
y=113−x
y=\\frac{11}{3}-x。
-
接上面的题目
求一个向量
b
b使得最小二乘求得的[C^D^]=[00]\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}=\\begin{bmatrix}0\\\\0\\end{bmatrix}:我们知道最小二乘求出的向量[C^D^]
\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}使得A
A列向量的线性组合最接近bb向量(即b
b在AA列空间中的投影),如果这个线性组合为0
0向量(即投影为00),则b
b向量与AA的列空间正交,所以可以取b=⎡⎣⎢1−21⎤⎦⎥
b=\\begin{bmatrix}1\\\\-2\\\\1\\end{bmatrix}同时正交于A
<script type="math/tex" id="MathJax-Element-275">A</script>的两个列向量。







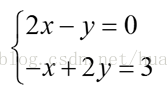





暂无评论内容