几年前把MIT Gilbert Strang教授的线性代数看完了,不过没做笔记,很多东西都忘了,现在打算重新看一遍,边写边做笔记。不足之处请指教。
—————————————————————————————————————————————————————————————————————————————
第一讲:方程组的几何解释
1. 方程组
对于方程组:
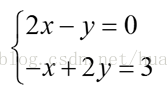
我们可以用矩阵进行表示:

系数矩阵 A,未知数向量 x,右侧向量为b,则可写成Ax=b。
1.1 行图像的理解方式
试图将每一个完整方程所表示的图像表示出来。
![图片[1]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130427-6395d55bbd201.png)
交点即方程的解为(1,2)
1.2 列图像的理解方式
关注矩阵的列所表示的向量,把两个方程组放在一起考虑:
![图片[2]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130427-6395d55bddd4e.png)
![图片[2]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130427-6395d55bf3c8c.png)
这样做的目的是找到两个列向量的正确的线性组合为右侧向量 ,现在需要求 x,y 这两个数值,来制造向量
(0,3),其几何形式,图像如下
![图片[3]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55c15c32.png)
选取所有的 x 和 y,即所有的线性组合即为整个坐标平面。可以求出右侧任意的 b 向量。
思考的范围扩展到3维:
![图片[4]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55c38bfb.png)
![图片[4]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55c4eb72.png)
如果以行(row)的形式进行展开的话,则在三维空间中每一行所表示的即为一一个平面。则其意义为求三个平面的交点,这个交点也就是方程组的解。图过于复杂就不画了。
而对应其以列(column)的形式进行展开:
![图片[5]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55c6e068.png)
其所表示的意义为三个向量的线性组合。
2.方程组解的情况
对于上面 3 维空间的例子,
保证左侧矩阵不变,然后考虑所有右侧向量,任意 b,是否每个 b 都有对应解?
换种说法:列的线性组合是否能覆盖整个三维空间?
非奇异矩阵,可逆矩阵可以做到。
如果是奇异矩阵,即不可逆矩阵,在行图像中看即至少有两个方程组所表示的平面是平行的,在列图像中
看即至少有两个列向量是指向同一方向的(即不相互独立,相当于同一个向量),此时,只有 b 处在这个
向量和另一个非共线向量所表示的平面内时,方程组才有解。
3. 矩阵与向量相乘的方法
3.1. 将矩阵 A 与向量 x 的相乘,看着 A 各列的线性组合,这是极力推荐的。
![图片[6]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55c8e114.png)
矩阵乘以右侧列向量可看成矩阵各列向量的线性组合,结果为列向量
左侧行向量乘以矩阵可看成矩阵各行向量的线性组合,结果为行向量!
3.2 以方程形式进行运算(常规的矩阵乘法)
![图片[7]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55caec75.png)
—————————————————————————————————————————————————————————————————————————————
第二讲: 矩阵消元
本课时的目标是用矩阵变换描述消元法。核心概念是矩阵变换。
1. 消元法(Elimination)
消元法:将主对角线上的主元固定(0 不能做主元),把主元下面的元素消为 0。过程:先完成左侧矩阵的消元(变成上三角矩阵 upper triangular system),再回代运算右侧向量,最后即可求出解完成整个消元过程。(matlab 也是先计算左侧矩阵,再回头计算右侧向量的)
1.1 消元法(success)
![图片[8]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55cca799.png) Ax=b,其中A即系数矩阵:
Ax=b,其中A即系数矩阵:![图片[8]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130428-6395d55ce37fe.png)
左侧矩阵的消元过程:U 矩阵是 A 矩阵的最终消元结果,最终得到上三角矩阵(upper triangular system)
![图片[9]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130429-6395d55d02a02.png)
1.2 消元法(failure)
消元法失效的情况(指不能得到三个主元):当主元上为 0 时,就通过交换行将主元位置变为非 0,当通过交换行还不能解决 0 主元的时候,消元法就失效了。(不能解决 0 主元的矩阵是不可逆矩阵)。
2. 回代(back substritution)
在方程组进行消元后,想要求出其解还需进行回代这一步。为了表示方便我们仍然使用系数矩阵,同时在这里引入新的矩阵为增广矩阵。引入增广矩阵的目的是为了使Ax = b中的b也随着系数矩阵的变换而变换,从而实现回代。
上图右侧向量回代过程:A 中加入 b 列向量变成增广矩阵,增广就是增加的意思,增加了新列,左侧矩阵消元时,右侧向量也会跟着变化。c 向量是b 向量的最终结果(c is what happens tob, andU is what happens toA)

求解:将 U 和 c 代入原式子可得解,利用上面解出的Ux=c

3. Elimination matrices(消元矩阵,row 是行,column 是列)
(引入矩阵描述这些(消元步骤的)变化(消元矩阵),用矩阵语言描述整个消元过程。)
回忆下我们应该怎样看待矩阵乘法(左行右列):
矩阵乘以列向量是矩阵列的线性组合,结果为列向量;行向量乘以矩阵式矩阵行的线性组合,结果为行向
量。
![图片[10]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130429-6395d55da2235.png)
![图片[10]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130429-6395d55dd6447.png)
这两张图是重点,是做矩阵消元的基础。
下面给一个例子:
![图片[11]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130430-6395d55e191b8.png) =
=![图片[11]-MIT 线性代数(1—3)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130430-6395d55e2f81e.png) =
=![图片[11]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124125625783.png)
然后:
![图片[12]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124125709339.png)
的结果是:
![图片[13]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124125716143.png)
![图片[14]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124125722214.png)
下面用消元矩阵来对矩阵进行消元,注意变换过程我们应该始终用线性组合的方式进行思考。同时注意到:
单位矩阵是一个不会对任何矩阵有任何变换作用的矩阵。
3.1 第一步
第一步消元:我们要对中间的矩阵进行消元,得到右侧矩阵,第一步为 row2=row2-3*row1。依次考虑左侧矩阵的行,第一行与中间矩阵的各个行向量进行线性组合,右侧矩阵的第一个行向量就是这个线性组合的结果,可观察容易得出左侧消元矩阵第一行为(1 0 0)。其实只需要由变换(row2=row2-3*row1)可得,消元矩阵中只有第二行有不同于单位矩阵的数值,即(-3 1 0)。
![图片[15]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124123814384.png)
E_21是elementary矩阵,对第二行第一个数进行处理。
3.2 第二步

以上每一步消元都使用到一个初等矩阵进行变换,我们将这些初等矩阵变换步骤综合起来(为什么综合起
来?原因之一是更节省空间),即
![图片[16]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124124100269.png)
4. Matrix multiplication(矩阵乘法)
4.1 逆矩阵初知
有什么矩阵可以一次性完成 E32 和 E21 的消元任务呢?可以用结合律将 E32 和 E21 乘起来得到,但我们不这样做。
更好的方法:不是关于 A 怎么变换成 U,而是 U 如何变成 A,逆变换。下一课时将详细讲解。逆矩阵,右侧消元矩阵表示的变换是 row2 减去 3 倍 row1,将右侧向量从(2 12 2)变成(2 6 2)。现在需要将(2 6 2)通过找到某矩阵取消这次消元,减去多少就加回来多少,变回(2 12 2),即该矩阵乘以初等矩阵得到单位矩阵。
即:原矩阵是 A,E_1 A=B,E_2 E_1 A=E_2 B,A=E_2 B(E_2 会将B 变回A),I_A=E_2B,E_2 E_1=I,E_2 与E_1 互为逆矩阵。

4.2 置换(permutation)矩阵
置换(permutation)矩阵:即交换行或交换列的变换矩阵,用P表示。
行交换:
![图片[17]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124124737029.png)
列交换:
![图片[18]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170124124754014.png)
总结:
本课的重点内容是:1. 怎样形成上三角矩阵;
2. 左行右列的真正含义。
—————————————————————————————————————————————————————————————————————————————
第三讲:矩阵的乘法和逆矩阵(非奇异矩阵)
本课时先讲解矩阵乘法运算,然后是逆矩阵及如何通过增广矩阵求逆。
一、矩阵乘法:5种方法
A(m×n), B(n×p) =C(m×p),A 列必须等于 B 的行数,C=AB。
1.1 常规方法,行列点乘法
C=AB,C 中的第 i 行 j 列结果来自A 的第 i 行向量与 B 的第 j 列向量的点乘。整行整列的进行。即:
![图片[19]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126131924953.png)
1.2 列方法,整列考虑,列的线性组合方式
B 的一个列向量乘以 A(矩阵A 各列向量的线性组合)得到C 的对应列向量,此过程其余列向量暂不参与计算。即:
![图片[20]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126132211657.png)
1.3 行方法,整行考虑,行的线性组合方式
A 的一个行向量乘以 B(矩阵 B 各行向量的线性组合)得到C的对应行向量,此过程其余行向量暂不参与计算。
![图片[21]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126141133692.png)
1.4 列×行法:AB 等于 A 各列与 B 各行乘积之和
A 中列乘以 B 中行,如 A 第一列乘以 B 第一行得一个矩阵(这样的矩阵很特殊,行向量和列向量都是单个向量的线性组合,第四讲会讲到有关行空间,列空间的概念),最后将得到的各矩阵相加。我们就看一列和一行相乘的例子:
![图片[22]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126141101632.png)
1.5 分块乘法
将矩阵 A,B 分成能够相互匹配的块,然后对应进行分块行点乘分块列。
![图片[23]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126141156133.png)
二. 矩阵的逆
2.1 定义
![图片[24]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126141530291.png)
2.2 判定逆矩阵
1)行列式为 0。
2)列图像思考,假设 A 可逆,那 A 乘以他的逆矩阵得单位矩阵,A 矩阵乘以其逆矩阵的第一列得单位矩阵的第一列(1 0),因为其列的线性组合始终在(1 2)这条直线上,所以不可能得到(1 0)向量。

3)如果存在非 0 向量 x,使的 Ax=0,即 x 对 A 的列向量的线性组合可以得到 0 向量(有一列在线性组合中不起作用),那么 A 是不可逆的。证明:假设存在可逆矩阵 A^-1,那么有A^-1Ax=0,得 Ix=0,得x=0,与x是非 0 向量相违背。
结论:不可逆矩阵,奇异矩阵,其列能通过线性组合得到 0 向量。
2.3 求解矩阵的逆
1)利用列的线性组合思想,矩阵 A 乘以该求的逆矩阵得到单位矩阵,这样,求逆和求方程组是一个意思
![图片[25]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126142518774.png)
2)将两个方程组放在一起考虑,如下,可理解为系数矩阵不变,分别求两个方程组的解,即可求得矩阵的逆。我们把下面两个放在一起考虑,形成增广矩阵,使得消元变换对两个方程组的作用是一样的。将增广矩阵的左侧变换消元为单位矩阵,右侧就变成其逆矩阵了。这是高斯-若尔当思想消元。
![图片[26]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126142533545.png)
为什么增广矩阵的右侧变成的是矩阵 A 的逆,以下变换给予证明:E 为一次性的消元矩阵,EA=I,那么E=A^-1 了。
![图片[27]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126143103876.png)
2.4 A 和 B 都存在逆,那么 AB 的逆是多少?
答案是: B 的逆乘以 A 的逆得到的矩阵。为什么相乘的顺序要反过来?因为逆即是逆操作。
![图片[28]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126143334424.png)
2.5 可逆矩阵转置的逆是什么?
A 乘以 A 的逆等于单位矩阵,两侧同时转置,右侧单位矩阵转置仍然得单位矩阵,左侧分别转置两个矩阵,
然后以相反顺序相乘,因此 A 的逆的转置乘以 A 的转置得到单位阵。A 转置的逆即是 A 的逆的转置。因
此,要求 A 转置的逆,只需要先求 A 的逆,然后求该逆的转置即可。转置和逆两种乘法运算,对于单个矩
阵而已,其顺序可以颠倒。
![图片[29]-MIT 线性代数(1—3)读书笔记-卡核](wp-content/uploads/2022/12/20170126143555241.png)
总结:
1. 矩阵乘法的五种形式。
2. 矩阵逆的定义和求法。
3. 矩阵AB的逆和A转置的逆。
———————————————————————————————————————————————————-
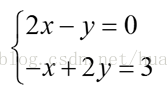









![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








