在知识传播途中，向涉及到的相关著作权人谨致谢意！

栅格数据结构

1. 点：为一个像元
2. 线：在一定方向上连接成串的相邻像元集合
3. 面：聚集在一起的相邻像元集合。

【一个完整的栅格模型需要以下几个参数】

1. 栅格形状
2. 栅格单元尺寸大小/分辨率
3. 栅格原点
4. 栅格的倾角

【栅格单元大小】

【单元值的确定】

完全栅格数据结构

【原理】完全栅格数据结构（也称编码）将栅格看作一个数据矩阵，逐行逐个记录栅格单元的值
【方法】可以每行都从左到右，也可奇数行从左到右而偶数行从右到左，或者采用其他特殊的方法

【优点】

1. 它不采用任何压缩数据的处理，因此这是最简单、最直接、最基本的栅格组织方式
2. 通常这种编码为栅格文件或格网文件

普通栅格的存储方式

1. 基于栅格方式：以栅格为存储单元，只存一个矩阵，矩阵中的一个格子存多个属性值（层属性）
2. 基于层方式：以层为存储单元，存储多个矩阵，矩阵中的一个格子只存一个属性值
3. 基于面域的方式：以层为存储单位的基础上，再以多边形为存储单元，一个多边形存储它区域内的所有栅格值

多通道/多波段影像完全数据结构

1. BSQ（Band sequential）：按波段顺序依次排列的数据结构
2. BIP（Band interleaved by pixel）：每个像元按波段次序交叉排列
3. BIL（Band Interleaved by line）：逐行按波段次序排列的格式

压缩栅格数据结构

游程长度编码

【游程】相邻同值网格的数量
【游程长度编码结构】栅格数据无损压缩的重要方法
【基本思想】对于一幅栅格数据，常有行、列方向相邻的若干点具有相同的属性代码，因而采取某种方法压缩重复的个数
【目的】压缩栅格数据量，消除数据间的冗余
【压缩过程】叫二元组映射

四叉树数据结构

1. what：栅格数据压缩的方式
2. what：四分之一的划分，直到子区内属性相同

【思路】对栅格数据进行压缩的一种方法

1. 将一幅是栅格数据层分为四个部分，逐块检查格网属性值
2. 如果子区所有格网属性相同，则停止再分，此时该子区不论大小，均作为最后的存储单元。否则，便继续将子区分为4个子区，依次检查下去
   通过这样，实现对数据的压缩

常规四叉树

线性四叉树（Morton码）

• 线性四叉树则只存贮最后叶结点的信息，包括叶结点的位置编码/地址码、属性或灰度值
• 线性四叉树地址码，通常采用十进制Morton码（MD码）

【优点】

1. 压缩效率高，压缩和解压缩比较方便
2. 阵列各部分的分辨率可不同，既可精确地表示图形结构，又可减少存储量，易于进行大部分图形操作和运算

【缺点】不利于形状分析和模式识别，即具有图形编码的不定性
如同一形状和大小的多边形可得出完全不同的四叉树结构

【Morton码】

• MD码对一个位置进行唯一的标识

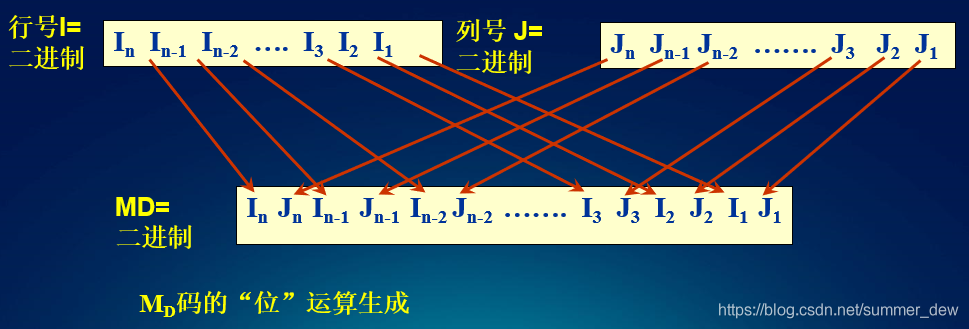
• 行列二进制进行交替获得一个二进制的MD码（列是第一位），然后再将二进制的MD码转成十进制

• [图1] MD码如何生成：列号先插，行列号交错
  

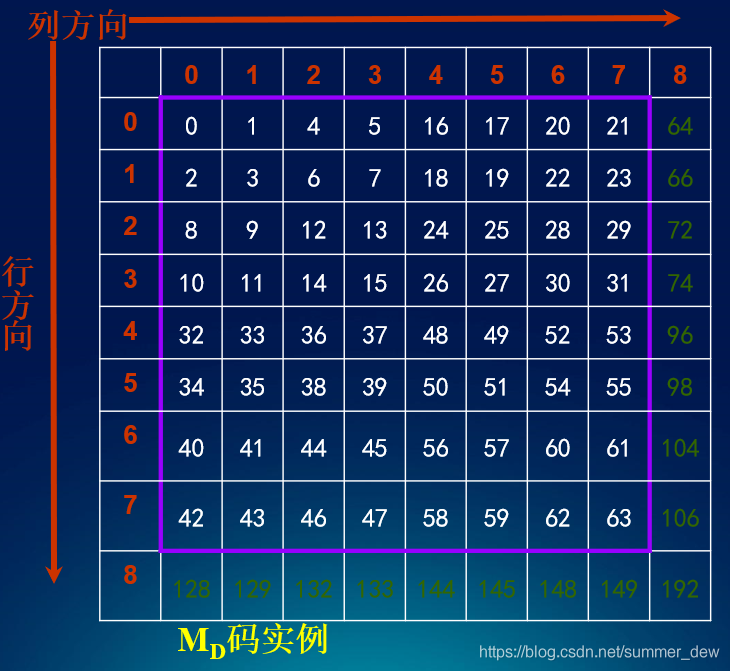
• [图2] MD码的实例（Z字形的一笔画法）
  

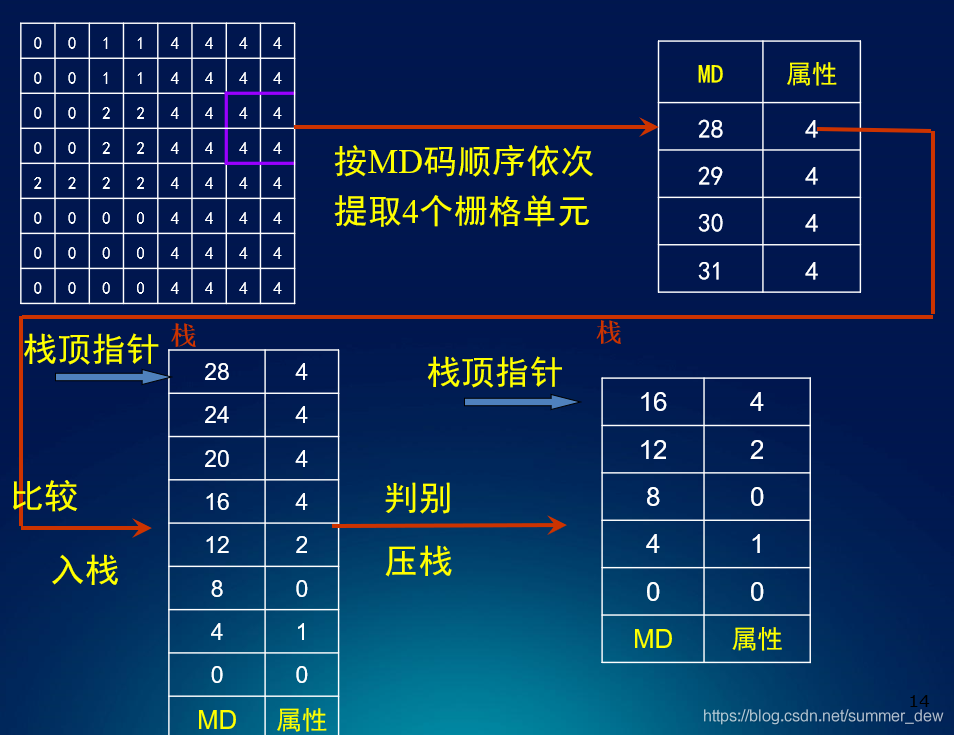
• [图3] 线性四叉树（MD码标识）的过程图
  

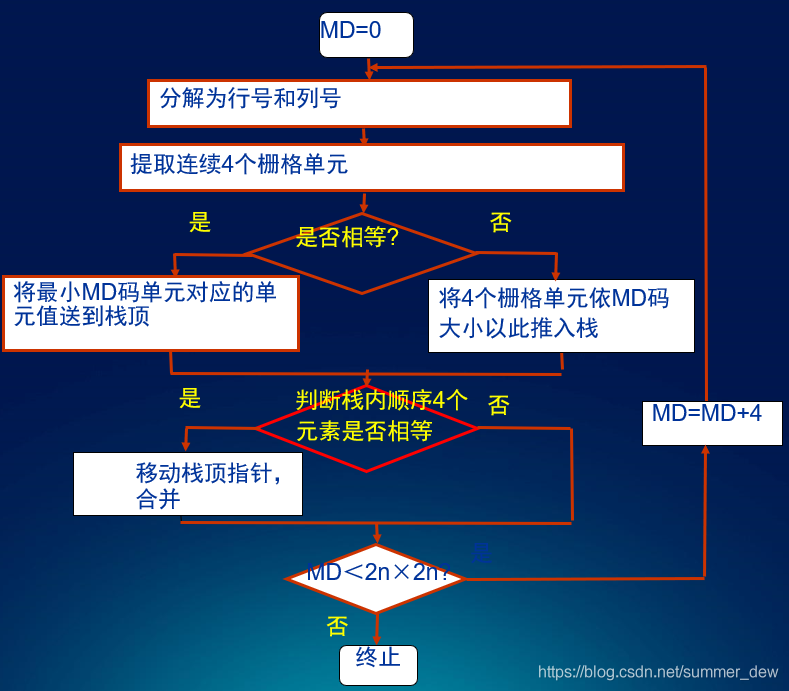
• [图4] 线性四叉树（MD码标识）的流程图
  

• [图5] 线性四叉树（Md码表示方法）结果图
  

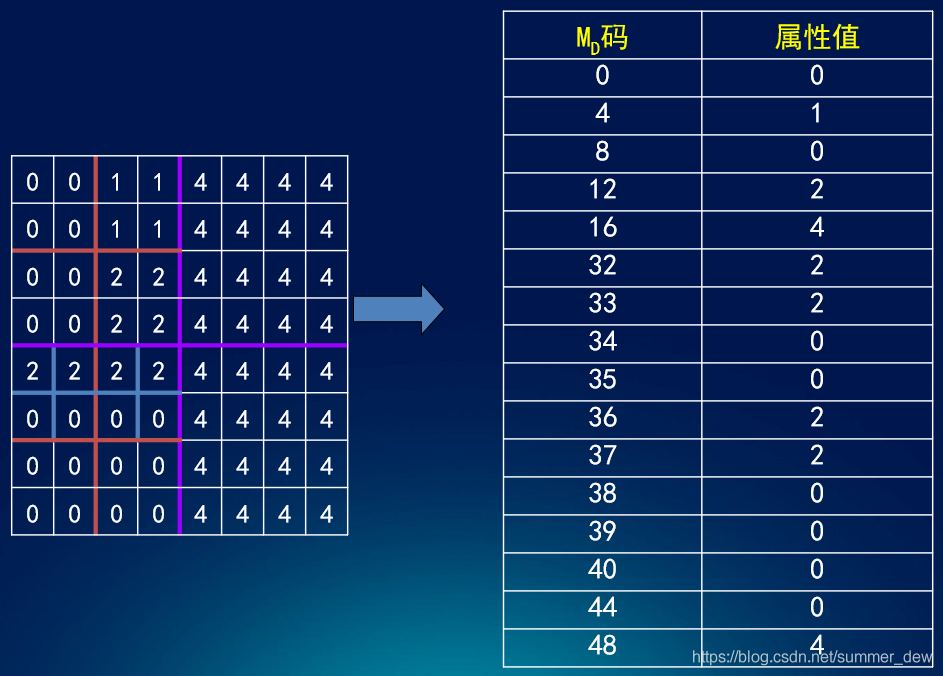
二维行程编码结构

对线性四叉树中仍存在前后叶结点相同值的情况，进一步压缩数据，将前后值相同的叶结点归并

【概念】类似于传统的一维行程编码，对应线性表先记录入口地址和格网值，一次扫描线性表。若后一格网值不等于前一格网的值，记录后一格网的地址码和相应的个格网值
【基本思想】

1. 将线性四叉树的线性表按四叉树的地址码（Morton码）的大小顺序排列
2. 出现属性值相同而又相邻排列的情况，将相同的叶节点合并得到二维行程编码结构

【优点】

1. 与规则的四叉树相比，二维行程编码结构又进一步压缩了数据，更节省存储空间
2. 有利于以后的插入、删除、修改等操作
3. 它与线性四叉树的相互转换也非常容易和快速，因此可将它们视为相同的结构概念

链码结构

链码数据结构首先采用弗里曼（Freeman）码对栅格中的线或多边形边界进行编码，然后再组织为链码结构

【优点】

1. 有效地压缩了栅格数据，尤其对多边形的表示最为显著
2. 链式编码还有一定的运算能力，对计算长度、面积或转折方向的凹凸度更为方便
3. 比较适于存储图形数据

【缺点】

1. 对边界做合并和插入等修改编辑工作很难实施
2. 对局部修改要改变整体结构，效率较低

影像金字塔数据结构

【影像金字塔结构】用于图像编码和渐进式图像传输，是一种典型的分层数据结构形式
【思想】在统一的空间参考下，根据用户需要以不同分辨率进行存储于显示，形成分辨率由粗到细、数据量由小到大的金字塔结构
【具体】在金字塔结构里，图像被分层表示

• 在金字塔结构的最顶层，存储最低分辨率的数据
• 随着金字塔层数的增加，数据分辨率依次降低
• 在金字塔的底层，则存储能满足用户需要的最高分辨率的数据

【优点】

1. 适合于栅格数据和影像数据的多分辨率组织
2. 也是一种栅格数据或影像数据的有损压缩方式 ，有M-金字塔，T-金字塔等