文章目录
【XJTUSE计算机图形学】第四章 真实感图形学(2)——简单光照明模型
简单光照明模型
光源
发射光源:反射表面
通常在一个不透明且不发光的物体表面所观察到的光线是其反射光,由光源与其他物体表面的反射光所共同产生。
光源向四周所辐射光的光谱分布
漫反射:投射在粗糙表面上的光向各个方向反射的现象。物体颜色实际上是入射光线被漫反射后所表现出来的颜色;
镜面反射:一束平行光射到平面镜上,反射光是平行的 。
空间的光亮度分布
图形学:光源通常朝空间各个方向发射的光强是相同的。
材质
材质的颜色是由它所反射的光的波长决定;
如果光线被投射到一个不透明的物体表面,则部分光线被反射,部分被吸收:
物体表面的材质类型决定了反射光的强弱;
表面光滑较亮的材质将反射较多的入射光,比较暗的表面则吸收较多的入射光。
对于一个半透明的物体表面,部分入射光会被反射,部分则被折射。
光照射到物体表面,可能被吸收、反射和透射
被吸收的部分转化为热;
反射、透射光进入人的视觉系统。
光照明模型:模拟物体表面的光照明物理现象的数学模型。
简单光照明模型
只考虑光源对物体的直接光照;
景物表面常被假定为不透明,且具有均匀反射率;
能表现由光源直接照射在漫射表面上形成的连续明暗色调,镜面上的高光以及由于景物互相遮挡而形成的阴影等。
只考虑反射,不考虑折射
发展历程
1967年,Wylie等人第一次在显示物体时加进光照效果,并假设光强与距离成反比;
1970年,Bouknight提出第一个光反射模型:Lambert漫反射+环境光;
1971年,Gouraud提出漫反射模型加插值的思想;
1975年,Phong提出图形学中第一个有影响的光照明模型。
相关物理知识
光的传播
反射定律:入射角等于反射角,而且反射光线、入射光线与法向量在同一平面上。
折射定律:折射线在入射线与法线构成的平面上,折射角与入射角满足
η
1
η
2
=
s
i
n
φ
s
i
n
θ
\\frac{\\eta_1}{\\eta_2}=\\frac{sin \\varphi}{sin \\theta}
η2η1=sinθsinφ
能量关系:在光的反射和折射现象中,能量是守恒的,能量的分布情况满足这样的一个式子:
I
i
=
I
d
+
I
s
+
I
t
+
I
v
I_i =I_d+I_s+I_t+I_v
Ii=Id+Is+It+Iv
I
i
I_i
Ii为入射光强,由直接光源或间接光源引起;
I
d
I_d
Id为漫反射光强,由表面不光滑引起;
I
s
I_s
Is为镜面反射光强,由表面光滑性引起;
I
t
I_t
It为透射光,由物体的透明性引起;
I
v
I_v
Iv为被物体所吸收的光,由能量损耗引起
光的度量
立体角:面元ds向点光源P所张的立体角为:
d
ω
=
d
s
r
2
d \\omega =\\frac{ds}{r^2}
dω=r2ds
r为点光源到面元中心的垂直距离
点发光强度
光通量:单位时间内通过面元ds的光能量,记为dF 。
发光强度:点光源的发光强度为某个方向上单位立体角的内的光通量,即
各向同性的点光源,在各个方向上单位立体角内通过的光通量相等,即在各个方向上发光强度相等;
设发光强度为*I,*则点光源向外辐射的整个光通量为整个球立体角内的光通量,即
Phong光照明模型
光照到物体表面时,物体对光会发生反射、透射、吸收、衍射、折射和干涉。
简单光照明模型模拟物体表面对光的反射作用
光源为点光源;
反射作用分为:镜面反射和漫反射;
物体间作用用环境光(Ambient Light)表示;
典型:Phong光照明模型。
Phong模型中的几何量示意图
理想漫反射
理想漫反射:当光源来自一个方向时,由于物体表面粗糙不平,导致反射光均匀向各方向传播,而与视点无关。
假设入射光强$I_p
,
物
体
表
面
上
点
P
的
法
向
为
N
,
从
点
P
指
向
光
源
的
向
量
为
L
,
两
者
夹
角
为
,物体表面上点P 的法向为N,从点P 指向光源的向量为L,两者夹角为
,物体表面上点P的法向为N,从点P指向光源的向量为L,两者夹角为\\theta$ ,由Lambert余弦定律,漫反射光强为:
K
d
K_d
Kd是与物体有关的漫反射系数
0
<
K
d
<
1
0<K_d<1
0<Kd<1
当L,N为单位向量时,漫反射光强可表示为:
有多个光源时,上式可进一步表示为
反射光颜色:由入射光颜色和物体表面颜色共同决定;
在RGB颜色模型下, 有三个分量,分别代表三原色的漫反射系数,通过调整它们来设定物体的颜色;
可以把入射光强I设为三个分量
I
r
,
I
g
,
I
b
I_r,I_g,I_b
Ir,Ig,Ib,通过这些分量的值来调整光源的颜色
镜面反射光
理想镜面:反射光集中在一个方向并遵循反射定律。
光滑表面:反射光集中在一个范围内,且由反射定律决定的反射方向光强最大。对于同一点,不同位置观察到的镜面反射光强不同。
镜面反射光强:
K
s
K_s
Ks是与物体有关的镜面反射系数;
α
\\alpha
α为视线方向V与反射方向R的夹角;
n为反射指数,反映物体表面的光泽程度,一般为1至2000,数目越大物体表面越光滑;
若规范所有向量,则镜面反射光强为:
其中
多个光源时,镜面反射光强为:
镜面反射光将会在反射方向附近形成很亮的光斑,称为高光现象;
镜面反射光产生的高光区域只反映光源的颜色;
镜面反射系数 是一个与物体的颜色无关的参数;
只能通过改变物体的漫反射系数来控制物体的颜色。
环境光
环境光:光源间接对物体施加的明暗影响,是在物体和环境之间多次反射,最终达到平衡时的一种光
同一环境下的环境光光强均匀分布,即在任一方向上的分布相同;
在简单光照明模型中,近似表示为:
I
e
=
I
a
.
K
a
I_e=I_a.K_a
Ie=Ia.Ka
I
a
I_a
Ia :为环境光的光强;
K
a
K_a
Ka:为物体对环境光的反射系数。
Phong光照明模型:由物体表面上一点P反射到视点的光强
I
I
I为环境光的反射光强
I
e
I_e
Ie、理想漫反射光强
I
s
I_s
Is和镜面反射光
I
d
I_d
Id的总和
I
=
I
a
K
a
+
I
p
K
d
(
L
.
N
)
+
I
p
K
s
(
R
.
V
)
n
I=I_aK_a+I_pK_d(L.N)+I_pK_s(R.V)^n
I=IaKa+IpKd(L.N)+IpKs(R.V)n
K
d
K_d
Kd是与物体有关的漫反射系数
0
<
K
d
<
1
0<K_d<1
0<Kd<1
入射光强$I_p $
I
a
I_a
Ia 为环境光的光强;
物体表面上点P 的法向为
N
N
N,从点P 指向光源的向量为
L
L
L,两者夹角为
θ
\\theta
θ
Phong模型:对物体表面上的每个点P,均需计算光线的反射方向R,再由R计算(R•V)。假设:
光源在无穷远处,即L为常向量;
视点在无穷远处,即V为常向量;
(H•N)近似(R•V) ,H为L与V的平分向量:
H
=
L
+
V
∣
L
+
V
∣
H=\\frac{L+V}{|L+V|}
H=∣L+V∣L+V。
对所有的点总共只需计算一次H的值
结合RGB颜色模型,Phong光照明模型

Phong光照明模型:真实感图形学中提出的第一个有影响的光照明模型,生成图像的真实度已达到可以接受的程度。
由于是经验模型,Phong模型存在不足:
显示出的物体像塑料,无质感变化;
环境光是常量,没有考虑物体间相互反射光;
镜面反射颜色是光源颜色,与材质无关;
镜面反射的计算在入射角很大时会产生失真现象。
增量式光照明模型
由于光源和视点均被假定为无穷远,Phong模型光强计算公式是物体表面法向量的函数。
用多边形表示的物体
每个多边形由于法向一致,多边形内部颜色相同;
不同法向的多边形邻接处光强突变且有马赫带效应
1868年由奥地利物理学家 E.马赫发现的一种明度对比现象:人们在明暗交界处感到亮处更亮,暗处更暗的现象;
生理学的解释:人类的视觉系统有增强边缘对比度的机制
增量式光照明模型:
在每个多边形顶点处计算光照明强度或参数,然后在各个多边形内部进行双线性插值,得到多边形光滑均匀颜色分布;
保证多边形之间的颜色光滑过渡。
两个主要算法(要会实质和步骤)
双线性法向插值:Phong明暗处理
双线性光强插值:Gouraud明暗处理
Gouraud双线性光强插值
Gouraud于1971年提出,又被称为Gouraud明暗处理;
思想:计算多边形各顶点的光强,再用双线性插值,求出多边形内部各点的光强
实质是:双线性光强插值
算法步骤的基本描述
1️⃣ 计算多边形顶点的平均法向;
2️⃣ 用简单光照明模型计算顶点的平均光强;
3️⃣ 插值计算离散多边形边上的各点光强;
4️⃣ 插值计算多边形内域中各点的光强。
顶点的计算
与某个顶点相邻的所有多边形的法向平均值近似作为该顶点的近似法向量;
顶点A相邻的多边形有k个,它的法向量计算为:

计算出的平均法向一般与该多边形物体近似曲面的切平面比较接近。
顶点平均光强计算
用Phong光照明模型及平均法向量计算在顶点A处的光强;
Gouraud提出明暗处理方法时,还未出现Phong模型,采用:
r是光源到顶点的距离;
l是防止分母趋于0的变量
双线性光强插值:线性插值与扫描线算法相互结合,用增量算法实现各点光强的计算
由顶点的光强插值计算各边的光强,然后由各边的光强插值计算出多边形内部点的光强:

增量算法

双线性光强插值
计算速度比以往的简单光照明模型有了很大的提高,解决了相邻多边形之间的颜色突变问题,产生的真实感图象颜色过渡均匀,图形显得非常光滑;
由于采用光强插值,镜面反射效果不太理想,而且相邻多边形的边界处的马赫带效应不能完全消除。
Phong双线性法向插值
实质是双线性法向插值,计算量比Gouraud大
以时间为代价,可以部分解决上述的弊病;
将镜面反射引进到明暗处理中,解决了高光问题
Phong双线性法向插值特点
保留双线性插值,对多边形边上的点和内域各点,采用增量法;
对顶点的法向量进行插值,而原顶点的法向量,仍用相邻多边形的法向作平均;
由插值得到法向,来计算多边形每个象素的光强度;
假定光源与视点均在无穷远处,光强只是法向量的函数。
方法与光强插值类似,其中的光强项用法向量项来代替。基本公式:

增量插值计算也类似,用法向代替光强。
两种模型的评价
两类模型的特点:
光强插值能有效的显示漫反射曲面,计算量小;
法向插值可产生正确的高光区域,但计算量大。
增量式光照明模型的不足:
此模型得到的物体边缘轮廓是折线段而非光滑曲线;
由于透视原因,等间距扫描线会产生不均匀效果;
插值结果决定于插值方向。
阴影
阴影
阴影是现实生活中一个很常见的光照现象;
在真实感图形学中,通过阴影可以反映出景物之间的相对位置,增加图形的立体效果和场景的层次感;
在建筑、航天飞行器设计的供热、太阳能计算等领域均有重要的应用
相关术语
接受物:可能接受光源照射的物体 。
本影:任意一点均无法观察到光源任何部分。
半影:任意一点可观察到部分光源。
阴影:即任意一点不能完全地观察到整个光源。
遮挡物:可遮挡光源中任意一点的物体。
Hard 阴影 vs Soft阴影
Hard阴影:点光源照射下,阴影问题是个二值状态
在计算机图形学中,很容易生成点光源,并且有一些生成Hard阴影的实时算法;
Hard阴影真实感较差。
Soft阴影:几乎不存在真正意义上的点光源
如太阳,其实也不是真正意义上的点光源,其所对应的阴影也不属于Hard阴影;
对于非点光源,计算本影和半影区域是非常复杂的过程。

阴影分类
自身阴影:光源被景物遮挡而在该景物本身;
投影阴影:在其后面产生的较暗的区域。

自身阴影
点光源下,生成产生具有自身阴影的步骤:
1️⃣ 将视点移到光源位置,将景物的面分成向光面和背光面;
2️⃣ 将视点移到原来的观察位置,对景物的向光面和背光面进行消隐,选用一种光照模型计算景物各面的亮度
3️⃣ 如果面在阴影区域,那么该面的光强就只有环境光那一项,其他的那几项光强都为零,否则就用正常的模型计算光强。
阴影算法与消隐算法相似:
消隐算法是根据视点看过去确定哪些面是可见的(前向面)或是不可见的(后向面)
而阴影算法则要确定哪些面从光源位置看过去是亮的(向光面)或暗的(背光面)。
从原理上,自身阴影面的求取只要简单地对消隐算法作出一点改造:
消隐算法中根据视向确定的那些后向面就是阴影算法中根据光源方向确定的那些背光面(自身阴影面)。
投影阴影
投射阴影的区域和形态与光源及景物的形状有很大的关系;
在光源的照射下,景物A在屏幕上产生了3个区域:本影区、半影区和无影区。

投射阴影区域:实际上是将光源作为观察方向时景物在与光源反向的某一平面上的落影区;
投射平面可以是场景中另一景物的表面或是一个非场景范畴的基面,如建筑物所在的地平面或屏幕等。
经典的三种本影阴影方法
1️⃣ 投影阴影;
2️⃣ 阴影图(Shadow Map)的方法;
3️⃣ 阴影体(Shadow Volume)的方法。
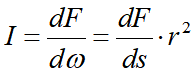

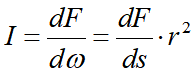







![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








