文章目录
【XJTUSE计算机图形学】第三章 几何造型技术(3)——B样条曲线与曲面
B样条曲线与曲面
Bezier曲线缺陷:
缺乏灵活性:一旦确定了多边形的顶点数,就确定了曲线的阶数;
控制性差:当顶点数较多,曲线的阶次将比较高,此时,特征多边形对曲线形状的控制将明显减弱;
不易修改:由曲线的方程可看出,其Bernstein基函数的值在开区间(0,1)内不为零。因此,所定义之曲线(0<t<1)在区间内的任何一点均要受到全部顶点的影响,这使得对曲线进行局部修改成为不可能。
B样条曲线:为克服Bezier曲线的缺陷,Gordon等人拓展了Bezier曲线,从外形设计的需求出发,希望新曲线易于进行局部修改、更逼近特征多边形、低阶次曲线
于是,用k阶B样条基函数替换了Bernstein基函数,构成了称之为B样条曲线的新型曲线。
B样条的递推定义与性质
基本概念
半开区间
[
t
i
,
t
i
+
1
]
[t_i,t_{i+1}]
[ti,ti+1] 是第i+1个节点区间;
集合T称为节点矢量;
重节点:如果一个节点ti出现r次 (即
t
i
=
t
i
+
1
=
.
.
.
=
t
t
+
r
−
1
,
r
>
1
t_i=t_{i+1}=…=t_{t+r-1},r>1
ti=ti+1=...=tt+r−1,r>1),ti 是重复度为r的多重节点
定义
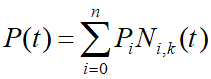
P
i
(
i
=
0
,
1
,
.
.
.
,
n
)
P_i(i=0,1,…,n)
Pi(i=0,1,...,n)是控制多边形的顶点
N
i
,
k
(
t
)
(
i
=
0
,
1
,
.
.
.
,
n
)
N_{i,k}(t)(i=0,1,…,n)
Ni,k(t)(i=0,1,...,n)称为k阶(k-1次)B样条基函数
多种基函数的定义:
de Boor-Cox递推定义
第i个k阶(基函数度数)B-样条基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)

约定
0
0
=
0
\\frac{0}{0}=0
00=0
通常称为de Boor-Cox递归公式;
如果次数为零(k= 1),这些基函数都是阶梯函数。

特殊观察
1️⃣ 基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)在
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上非零;
2️⃣ 在任何一个节点区间
[
t
i
,
t
i
+
1
)
[t_i,t_{i+ 1})
[ti,ti+1), 最多有k个(k-1)次基函数非零:
N
i
−
k
+
1
,
k
(
t
)
,
N
i
−
k
+
2
,
k
(
t
)
,
.
.
.
,
N
i
,
k
(
t
)
N_{i-k+1,k}(t),N_{i-k+2,k}(t),…,N_{i,k}(t)
Ni−k+1,k(t),Ni−k+2,k(t),...,Ni,k(t)

性质
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)是t的k阶多项式
1️⃣ 局部支撑性:
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)是在
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上的非零多项式

2️⃣ 权性(单位分解 )

3️⃣ 微分公式

4️⃣ 非负性:对所有的i,k和t,
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)是非负的
5️⃣ 重要结论
基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)是(k-1)次多项式的复合曲线,连接点在
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上的节点处;
在重复度r的节点处,基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)是
C
k
−
r
−
1
C^{k-r-1}
Ck−r−1连续的;
如果节点数目是(m+1),函数的阶数是k,控制点的个数是(n+1),则m=(n+k),即节点数等于控制点数+阶数
❓ 五个控制顶点的三次B样条曲线由几个节点构成
5+4=9
注意阶数=次数+1
B样条曲线类型的划分
两个标准:首末节点是否重合和节点的分布情况。
1️⃣ 首末节点是否重合
开曲线:曲线不会与控制折线的第一边和最后一边接触;图1
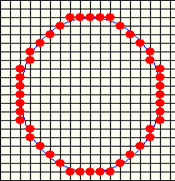
闭曲线:第1个节点和最后1个节点是重复节点。
–Clamped:第一个节点和最后一个节点必须是重复度为k ;图2
–Closed:重复某些节点和控制点。图3

2️⃣ 节点的分布情况
假定控制多边形的顶点为
P
i
(
i
=
0
,
1
,
.
.
.
n
)
P_i(i=0,1,…n)
Pi(i=0,1,...n),阶数为k(次数为k-1),则节点矢量为
T
=
[
t
0
,
t
1
,
.
.
.
,
t
n
+
k
]
T=[t_0,t_1,…,t_{n+k}]
T=[t0,t1,...,tn+k]
均匀样条曲线
节点矢量中节点为沿参数轴均匀或等距分布,所有节点区间长度为常数。这样的节点矢量定义了均匀的B样条基
节点矢量为[0, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 1]
准均匀样条曲线
两端点的重复度为k,内部其它节点呈均匀分布,且重复度为1。
端点过特征多边形的端点
节点矢量为[0, 0, 0, 0,1/3,2/3, 1,1, 1, 1]
分段Bezier曲线
节点矢量中两端节点具有重复度k,所有内节点重复度为k-1,这样的节点矢量定义了分段的Bernstein基。
图中有7个控制顶点,n=6,阶数为4,因此节点数为6+4+1=11,节点矢量为
T
=
[
t
0
,
t
1
,
.
.
.
,
t
10
]
=
[
0
,
0
,
0
,
0
,
0.5
,
0.5
,
0.5
,
1
,
1
,
1
,
1
]
T=[t_0,t_1,…,t_{10}]=[0,0,0,0,0.5,0.5,0.5,1,1,1,1]
T=[t0,t1,...,t10]=[0,0,0,0,0.5,0.5,0.5,1,1,1,1]
一般的非均匀B样条曲线
B样条曲线的性质
局部性
1️⃣ k阶B样条曲线上参数为
t
∈
[
t
i
,
t
i
+
1
]
t\\in [t_i,t_{i+1}]
t∈[ti,ti+1]的一点至多与k个控制顶点
P
j
(
j
=
i
−
k
+
1
,
.
.
.
i
)
P_j(j=i-k+1,…i)
Pj(j=i−k+1,...i)有关,与其它控制顶点无关;
2️⃣
P
i
P_i
Pi只影响在区间
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上的曲线P(t);
基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)在
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上非零;
3️⃣ 基函数
N
i
,
k
(
t
)
N_{i,k}(t)
Ni,k(t)在区间
[
t
i
,
t
i
+
k
)
[t_i,t_{i+k})
[ti,ti+k)上都是次数不高于(k-1)的多项式。
❓ 改变一条以P0,P1,…,P9为控制顶点的4阶B样条曲线的一个顶点P5,有几段曲线的形状会改变?
P5影响在区间
[
t
5
,
t
9
)
∈
[
t
3
,
t
10
]
[t5,t9)\\in[t3,t10]
[t5,t9)∈[t3,t10]上的曲线,影响了4段曲线[t5,t6)、[t6,t7)、[t7,t8)、[t8,t9)
注意看定义域,可能有陷阱
开曲线定义域
有k个基函数的支持,定义域是
[
t
k
−
1
,
t
n
+
1
]
[t_{k-1},t_{n+1}]
[tk−1,tn+1](k-1是次数,n+1是控制顶点数)
举例
使用节点向量T={0,0.25,0.5,0.75,1},如果基函数是2阶的(即k=2),那么有三个基函数N0,2(t),N1,2(t)和N2,2(t);
第一个和最后一个节点区间只有一个非零基函数,而第二和第三节点区间(即[0.25,0.5)和[0.5,0.75))有两个非零基函数。
节点区间[0,0.25)和[0.75,1)没有基函数的“完全支持”。
一般来说,区间
[
t
0
,
t
k
−
1
)
[t_0,t_{k-1})
[t0,tk−1)和
[
t
n
+
1
,
u
n
+
k
]
[t_{n+1},u_{n+k}]
[tn+1,un+k]不会有基函数的“完全支持”,当B样条曲线是开曲线时被忽略。
凸包性

贝塞尔曲线是B样条曲线的特例

分段参数多项式
P(t)在每一区间上都是次数不高于k-1的参数t的多项式,因此P(t)是参数t的次数不高于k-1的分段多项式。
连续性

导数公式

变差缩减性

仿射不变性

即在仿射变换下,P(t)的表达式具有形式不变性。
如果一个仿射变换应用于B样条曲线,得到的结果可以从它的控制点的仿射像构建得到。
几何不变性
由于定义式所表示的B样条曲线是参数形式,因此,B样条曲线的形状和位置与坐标系选择无关。
直线保持性
控制多边形退化为一条直线时曲线也退化为一条直线
习题
1️⃣ 五个控制顶点的三次B样条曲线由几个节点构成
5+4=9
2️⃣ 一条以P0,P1,P2,P3,P4为控制顶点的4阶(三次)B样条曲线,其节点向量为{0,0,0,1,2,3,4,4, 4},则其定义域为?

3️⃣ 由五个控制顶点所决定的3次B样条曲线,由几段3次B样条曲线段光滑连接而成?
定义域是
[
t
3
,
t
5
]
[t3,t5]
[t3,t5],有两段连接
4️⃣ 改变一条以P0,P1,…,P9为控制顶点的4阶B样条曲线的一个顶点P5,有几段曲线的形状会改变?
P5影响在区间
[
t
5
,
t
9
)
∈
[
t
3
,
t
10
]
[t5,t9)\\in[t3,t10]
[t5,t9)∈[t3,t10]上的曲线,影响了4段曲线[t5,t6)、[t6,t7)、[t7,t8)、[t8,t9)
De Door算法(了解)

de Boor 算法的递推关系如图

三次B样条的Bezier表示(了解)

节点插入算法
进一步改善B样条曲线的局部性质,提高曲线的形状控制的灵活性,可实现对曲线的分割等
给定一条k阶B样条曲线$P(t)=\\underset{i=0}{\\overset{n}{\\sum}}P_i N_{i,k}(t)
,
B
样
条
基
由
节
点
矢
量
,B样条基由节点矢量
,B样条基由节点矢量T={[t_0,t_1,…,t_{n+k}]}$完全决定
插入一个节点
在定义域某个节点区间
[
t
i
,
t
i
+
1
]
[t_i,t_{i+1}]
[ti,ti+1]内插入一个节点t,得到新的节点矢量:
T
1
=
[
t
0
,
t
1
,
.
.
.
,
t
i
,
t
,
t
i
+
1
,
.
.
.
,
t
n
+
k
]
T^1={[t_0,t_1,…,t_i,t,t_{i+1},…,t_{n+k}]}
T1=[t0,t1,...,ti,t,ti+1,...,tn+k]
重新编号成为:
T
1
=
[
t
0
1
,
t
1
1
,
.
.
.
,
t
i
1
,
t
i
+
1
1
,
t
i
+
2
1
,
.
.
.
,
t
n
+
k
+
1
1
]
T^1={[t_0^1,t_1^1,…,t_i^1,t_{i+1}^1,t_{i+2}^1,…,t_{n+k+1}^1]}
T1=[t01,t11,...,ti1,ti+11,ti+21,...,tn+k+11]
新节点矢量T1决定了一组新B样条基
N
i
,
k
1
(
t
)
,
i
=
0
,
1
,
.
.
.
,
n
+
1
N_{i,k}^1(t),i=0,1,…,n+1
Ni,k1(t),i=0,1,...,n+1。原始的曲线可用这组新的B样条基与未知新顶点
P
i
1
P_i^1
Pi1表示
未知新顶点的计算公式(Boehm)
算法过程

B样条曲线的优点
优点:
可以是贝塞尔曲线;满足贝塞尔曲线有的所有重要性质;提供了比贝塞尔曲线更灵活的控制
曲线的次数与控制点数目是分开的,可使用更低次曲线而仍然保持很多控制点;
可以改变一个控制点位置而不会全局地改变整个曲线形状;
还有其他设计和编辑形状的技术比如改变节点。
B样条曲线仍然是多项式曲线,而多项式曲线不能表示许多有用的简单的曲线比如圆和椭圆。
B样条曲面

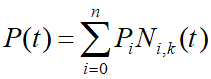









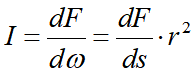


![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








