文章目录
【XJTUSE计算机图形学】第三章 几何造型技术(1)——参数曲线和曲面
几何造型技术
研究在计算机中,如何表达物体模型形状的技术;
70年代,已有不少实用化系统;
已应用于航空航天、汽车、机械、造船、建筑和电子等领域。
描述物体的三维模型: 线框模型、曲面模型、实体模型。
线框模型: 利用形体的顶点和棱边来表示物体。
曲面模型:通过有向棱边构成形体的表面,用面的几何表达相应的形体。
实体模型:定义一些基本体素,并通过集合运算将它们组合成复杂的几何形体。
参数曲线和曲面
曲线曲面参数表示
非参数表示
显式表示:y=f(x),无法表示封闭或多值曲线,如圆。
隐式表示:f(x,y)=0,易于判断函数值与零的关系,确定点与曲线的关系。
存在下述问题:
与坐标轴相关;
会出现斜率为无穷大的情形(如垂线)。
参数表示
参数表示:曲线上任一点的坐标均表示成给定参数的函数。假定用t表示参数
平面曲线上任一点P:
P
(
t
)
=
[
x
(
t
)
,
y
(
t
)
]
P(t)=[x(t),y(t)]
P(t)=[x(t),y(t)]
空间曲线上任一三维点P:
P
(
t
)
=
[
x
(
t
)
,
y
(
t
)
,
z
(
t
)
]
P(t)=[x(t),y(t),z(t)]
P(t)=[x(t),y(t),z(t)]
参数表示例子:
直线:
P
(
t
)
=
P
1
+
(
P
2
−
P
1
)
t
P(t)=P_1+(P_2-P_1)t
P(t)=P1+(P2−P1)t
圆:
P
(
t
)
=
[
1
−
t
2
1
+
t
2
,
2
t
1
+
t
2
]
P(t)=[\\frac{1-t^2}{1+t^2},\\frac{2t}{1+t^2}]
P(t)=[1+t21−t2,1+t22t]
参数表示的优点:
满足几何不变性的要求;
有更大的自由度来控制曲线、曲面的形状;
对参数方程进行几何变换即实现对曲线(面)的变换;
便于处理斜率为无穷大的情形;
参数方程中,代数、几何相关和无关的变量是完全分离的,且对变量个数不限,便于用户把低维空间中曲线、曲面扩展到高维空间去;
规格化的参数变量t∈[0,1],使其相应的几何分量是有界的,不必用另外的参数去定义边界;
易于用矢量和矩阵表示几何分量,简化了计算。
曲线的基本概念
1️⃣ 三维曲线
用参数表示的三维曲线是一个有界的点集,可以表示成一个带参数的、连续的和单值的数学函数:
{
x
=
x
(
t
)
y
=
y
(
t
)
,
0
≤
t
≤
1
z
=
z
(
t
)
\\left\\{ \\begin{array}{lc} x=x(t) \\\\ y=y(t),\\quad 0\\le t\\le 1\\\\ z=z(t) \\end{array} \\right.
⎩⎨⎧x=x(t)y=y(t),0≤t≤1z=z(t)
2️⃣ 位置矢量
曲线上任一点的位置矢量可表示为:
P
(
t
)
=
[
x
(
t
)
,
y
(
t
)
,
z
(
t
)
]
P(t)=[x(t),y(t),z(t)]
P(t)=[x(t),y(t),z(t)]
如存在k阶导数矢量,则:
P
k
(
t
)
=
d
k
P
d
t
k
P^k(t)=\\frac{d^kP}{dt^k}
Pk(t)=dtkdkP
3️⃣ 切矢量
选择弧长s作为参数,则 $T=\\frac{dP}{ds}=\\underset{\\Delta s \\to0}{\\lim}\\frac{\\Delta P}{\\Delta s} $ 是单位切矢量
根据弧长微分公式有:
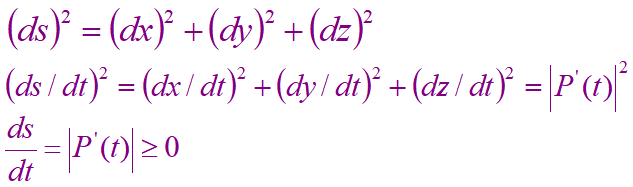
于是有
d
P
d
s
=
d
P
d
t
.
d
t
d
s
=
P
′
(
t
)
∣
P
′
(
t
)
∣
\\frac{dP}{ds}=\\frac{dP}{dt}.\\frac{dt}{ds}=\\frac{P'(t)}{|P'(t)|}
dsdP=dtdP.dsdt=∣P′(t)∣P′(t)
即T 为单位矢量
4️⃣ 法矢量
所有垂直于切矢量T 的矢量有一束,且位于法平面上
d
T
d
s
\\frac{dT}{ds}
dsdT是与T垂直的矢量;与
d
T
d
s
\\frac{dT}{ds}
dsdT平行的法矢称为曲线在该点的主法矢(N)
矢量积
B
=
T
×
N
B=T\\times N
B=T×N 是第三个单位矢量,它垂直于T和N。把平行于矢量B的法矢称为曲线的副法矢量;
可以推导出:

T(切矢)、N(主法矢)和B(副法矢)构成了曲线上的活动坐标架;
N、B构成的平面称为法平面,N、T构成的平面称为密切平面,B、T构成的平面称为从切平面。
5️⃣ 曲率和挠率
圆的半径越小,曲率越大



插值、拟合和光顺(掌握概念)
1️⃣ 插值: 给定一组有序的数据点Pi构造一条曲线顺序通过这些数据点,所构造的曲线称为插值曲线。
线性插值:
y
=
a
x
+
b
y=ax+b
y=ax+b
抛物线插值:
φ
(
x
)
=
a
x
2
+
b
x
+
c
\\varphi(x)=ax^2+bx+c
φ(x)=ax2+bx+c
2️⃣ 拟合:构造一条曲线使之在某种意义下最接近给定的数据点,所构造的曲线为拟合曲线。
3️⃣ 逼近:在计算数学中,逼近通常指用一些性质较好的函数近似表示一些性质不好的函数。在计算机图形学中,逼近继承了这方面的含义
包含插值和拟合
4️⃣ 过拟合:模型在训练集上效果很好,在测试集上效果差(不考)
5️⃣ 光顺(Fairing):指曲线的拐点不能太多。对平面曲线而言,相对光顺的条件是:
a. 具有二阶几何连续性(G2)
b. 不存在多余拐点和奇异点;
c. 曲率变化较小。
参数化
概念
过三点P0、P1和P2构造参数表示的插值多项式可以有无数条:
对应地参数t, 在[0,1]区间中有无数种取法;
参数值称为节点(knot)。
对于一条插值曲线,型值点
P
0
,
P
1
,
.
.
.
,
P
n
P_0,P_1,…,P_n
P0,P1,...,Pn与其参数域
t
∈
[
t
0
,
t
n
]
t\\in[t_0,t_n]
t∈[t0,tn]内的节点之间有一种对应关系:
对于一组有序的型值点,所确定一种参数分割,称之为这组型值点的参数化。
参数化常用方法
1️⃣ 均匀参数化(等距参数化);
节点在参数轴上呈等距分布,
t
i
+
1
=
t
i
+
正
常
数
t_{i+1}=t_i+正常数
ti+1=ti+正常数。
2️⃣ 累加弦长参数化;

反映型值点按弦长的分布情况;
能克服均匀参数化所出现的问题。
3️⃣ 向心参数化法;
4️⃣ 修正弦长参数化法。
参数区间的规格化
我们通常将参数区间
[
t
0
,
t
n
]
[t_0,t_n]
[t0,tn]规格化为[0,1],
[
t
0
,
t
n
]
≠
[
0
,
1
]
[t_0,t_n]\\not = [0,1]
[t0,tn]=[0,1],只需对参数化区间作如下处理:
t
0
=
0
,
t
i
=
t
i
t
n
,
i
=
0
,
1
,
.
.
.
,
n
t_0=0,\\ t_i=\\frac{t_i}{t_n},\\ i=0,1,…,n
t0=0, ti=tnti, i=0,1,...,n
参数曲线的代数和几何形式(了解一下)
以三次参数曲线为例,讨论参数曲线的代数和几何形式
代数形式

上述代数式写成矢量式是
几何形式
对三次参数曲线,可用其端点位矢P(0)、P(1)和切矢P¢(0)、P‘(1)描述。
将P(0)、P(1)、P’(0)和P‘(1)简记为P0、P1、P‘0和P’1,代入
 ,得
,得


令
简化为
上式是三次Hermite(Ferguson)曲线的几何形式
•几何系数:$ P_0、P_1、P’_0和P’_1$
•调和系数:
F
0
、
F
1
、
G
0
、
G
1
F_0、F_1、G_0、G_1
F0、F1、G0、G1

参数
F
0
,
F
1
F_0,F_1
F0,F1专门控制端点的函数值对曲线的影响;
参数
G
0
,
G
1
G_0,G_1
G0,G1专门控制端点的一阶导数值对曲线的影响。
连续性
设计制造时,组合多段曲线,因此需要解决曲线段之间的光滑连接问题。
曲线间连接的光滑度的度量(会考概念)
参数连续性:组合参数曲线在连接处具有直到n阶连续导矢,即n阶连续可微,称为n阶参数连续性
C
n
C^n
Cn
几何连续性:组合曲线在连接处满足不同于
C
n
C^n
Cn的某一组约束条件,称为具有n阶几何连续性
G
n
G^n
Gn。
介于n-1阶参数连续性和n阶参数连续性之间
同阶参数连续性的要求比几何连续性高
引进几何连续的重要性
🏷 举例

第
Φ
(
t
)
\\Phi(t)
Φ(t)在[0,2]上表示一条连接
V
0
,
V
1
V_0,V_1
V0,V1的直线段;
左右导数不等:
Φ
(
1
−
)
=
1
3
(
V
1
−
V
0
)
,
Φ
(
1
+
)
=
2
3
(
V
1
−
V
0
)
\\Phi(1^-)=\\frac{1}{3}(V_1-V_0),\\ \\Phi(1^+)=\\frac{2}{3}(V_1-V_0)
Φ(1−)=31(V1−V0), Φ(1+)=32(V1−V0)
参数连续描述光滑性不恰当。
举例说明
对于参数
t
∈
[
0
,
1
]
t\\in [0,1]
t∈[0,1]的两条曲线P(t)和Q(t)

1️⃣ 若要求在结合处达到
C
0
C^0
C0连续或
G
0
G^0
G0连续,即两曲线在结合处位置连续:
P
(
1
)
=
Q
(
0
)
P(1)=Q(0)
P(1)=Q(0)
2️⃣ 若要求在结合处达到
G
1
G^1
G1连续,就是说两条曲线在结合处在满足
G
0
G^0
G0连续的条件下,并有公共的切矢
Q
′
(
0
)
=
α
P
′
(
1
)
(
α
>
0
)
Q'(0)=\\alpha P'(1)\\qquad (\\alpha >0)
Q′(0)=αP′(1)(α>0)
当
α
=
1
\\alpha = 1
α=1时,
G
1
G^1
G1连续就成为
C
1
C^1
C1 连续
若P 和Q 在连接处已有
C
0
C
1
C^0 C^1
C0C1连续性且曲率的大小和方向均相等,即
P
′
′
(
1
)
=
Q
′
′
(
0
)
P''(1)=Q''(0)
P′′(1)=Q′′(0)则P 和Q 在连接处具有
C
2
C^2
C2连续
若P 和Q 在连接处已有
C
0
C
1
C^0 C^1
C0C1连续性且曲率的大小不相等但方向相等,则P 和Q 在连接处具有
G
2
G^2
G2连续。
3️⃣ 若要求在结合处达到
G
2
G^2
G2连续,就是说两条曲线在结合处在满足
G
1
G^1
G1连续的条件下,并有公共的曲率矢:

这个关系可写为
β
\\beta
β为任意常数,当
α
=
1
,
β
=
0
\\alpha =1 , \\beta = 0
α=1,β=0时,
G
2
G^2
G2连续就成了
C
2
C^2
C2连续
参数曲面基本概念
一张定义在矩形域上的参数曲面可以表示为

可记为
曲面上的点:将给定的参数值
u
0
,
v
0
u_0,v_0
u0,v0代入参数方程,可得曲面上的点
P
(
u
0
,
v
0
)
P(u_0,v_0)
P(u0,v0)
曲面上一点的切向量(切矢):
∂
P
(
u
,
v
)
∂
u
∣
u
=
u
0
,
v
=
v
0
∂
P
(
u
,
v
)
∂
v
∣
u
=
u
0
,
v
=
v
0
\\frac{\\partial{}P(u,v)}{\\partial{}u}|u=u_0,v=v_0 \\qquad \\frac{\\partial{}P(u,v)}{\\partial{}v}|u=u_0,v=v_0
∂u∂P(u,v)∣u=u0,v=v0∂v∂P(u,v)∣u=u0,v=v0
曲面上一点的法向(法矢):
角点:
P
(
0
,
0
)
,
P
(
0
,
1
)
,
P
(
1
,
0
)
,
P
(
1
,
1
)
P(0,0),P(0,1),P(1,0),P(1,1)
P(0,0),P(0,1),P(1,0),P(1,1)
边界线:
P
(
u
,
0
)
,
P
(
u
,
1
)
,
P
(
0
,
w
)
,
P
(
1
,
w
)
P(u,0),P(u,1),P(0,w),P(1,w)
P(u,0),P(u,1),P(0,w),P(1,w)

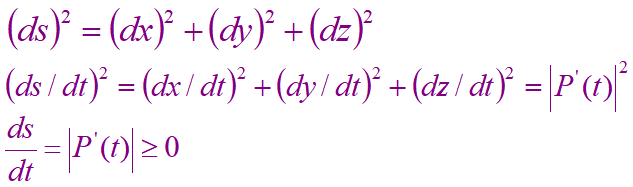





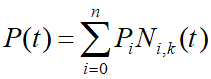


![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








