B-样条曲线：修改节点

B-spline Curves: Modifying Knots

上一页移动控制点             回目录                       下一页B-样条曲线的导数

因为B-样条曲线是许多曲线段的组合，每个定义于一个节点区间上，修改一个或多个节点位置会改变相应的曲线段和节点区间，因此改变曲线的形状。

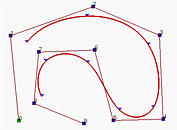
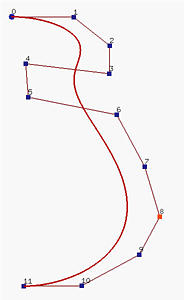
下图描述了修改一个单节点的效果。它是一个6次B-样条曲线，有17个节点，最前7个和最后7个在端点上是clamped，而内部节点是0.25, 0.5 和 0.75。初始曲线在左图显示。如果节点0.25 移动到0.1，曲线的形状改变，原来的C(0.25)向下移动到一个新位置。如果节点0.5移动到 0.1使得节点0.1变成一个双重节点 (重复度2)，曲线的形状移动到左边；但是C(0.1) 向上移动到接近原始点(即，原来的 C(0.25))的位置。结果显示在右图。尽管我们在 0.1 有一个双重节点以及在0.75另一个节点非均匀地将定义域[0,1] 划分成三个节点区间，B-样条曲线被它们相应点几乎均匀地划分。

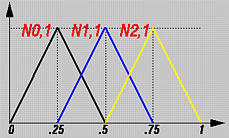
下图显示了三条曲线的形状的改变，每个由 10 (n=9)个控制点定义，次数是6。它们内部节点向量是 (0.25,0.5,0.75) – 红色曲线， (0.25,0.25,0.75) – 蓝色曲线， (0.25,0.25,0.25) -黑色曲线。

实际经验告诉我们修改节点位置不仅不可预测而且不令人满意。更准确地说，因为不清楚B-样条曲线会对节点向量的改变作怎样的反应，通过改变节点来修改B-样条曲线 通常都不令人满意而且很难达到设计目的。 

关于多重节点的评注 多重节点对产生期望的结果有帮助。回忆前面讨论的多重节点的性质，增加一个内部节点的重复度会减小在该节点的非零基函数的数目。实际上，如果该节点的重复度是 k, 最多在该节点上有 p – k + 1 个非零函数。而且，在该节点的基函数是C^p-k 连续的。

假设一个节点有重复度 p–k,在该节点上有k+1 个非零基函数且曲线上的相应点位于由控制点（与那些非零基函数相对应）定义的凸包内。如果 k = p – 1, 有两个非零函数而相应的凸包是直线段。

如果 k = p, 只有一个非零基函数在该节点上，只有一个控制点有非零系数。结果，曲线通过该点。

(a)	(b)	(c)

(d)	(e)

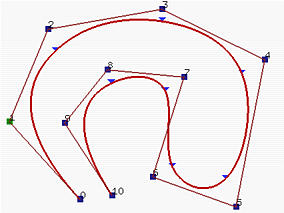
上面图 (a)，显示了一个5次B-样条曲线，相对应于标记的节点点的节点移动到它前面的节点，构建了一个重复度2的节点。结果在图 (b), 其与原始图没有太大差别。然后，下一个节点 (用矩形框标记)也被移动到产生的节点 ，构建了一个重复度3的节点。产生的曲线朝控制折线的一条边移动。再移动一个节点构建一个重复度4的新节点。这使得相应的点（椭圆标记）位于一条边上。最后，仅剩的一个节点移到与其它节点结合起来。由于它的重复度是5而 p=5, 只有一个非零系数因此使得曲线通过该控制点。如图(e)所示，该控制点是P₅ 。