学习openfoam的第四周。这次花两天时间来将userguide的第二个教程过一遍！
1. 案例解析
中文翻译是“带洞盘的压力分析”。在这个案例中，被分析对象的物理模型如下图所示：
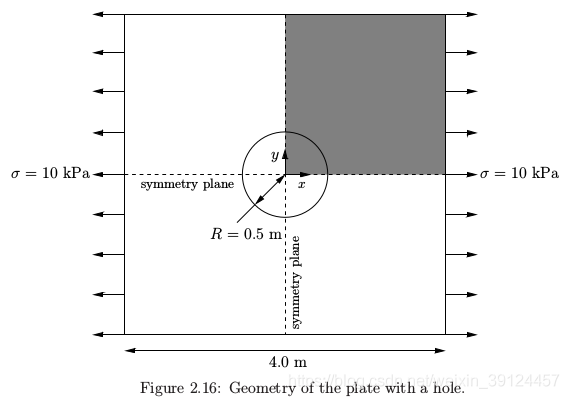
如图所示，在一个边长米的正方形盘子中央有一个半径为0.5m的洞。盘子两边施加均匀的牵引力。因为对称的关系，我们只需要分析盘子的四分之一（a quarter）即可。
这个问题可以被近似为一个2维问题。在一个理想情况下（盘子无限大，无限薄），这个问题是有解析解的：
这个tutorial可以帮助我们比较仿真和理论解的差别。因为仿真下我们设置的条件不是理想的。通过修改一些参数，我们也可以借此找找openfoam的感觉，包括网格分辨率和坡度的敏感程度，或者增大盘子的尺寸对结果带来的影响。
2. 网格生成
老规矩，先转到run文件夹，再将教程文件复制过来，代码：
cd OpenFOAM/foamer-4.1/run/
cp -r /opt/openfoam4/tutorials/stressAnalysis/solidDisplacementFoam/plateHole plateHole看看里面有什么：
打开system文件夹里的blockMeshDIct，可以看到设置的顶点，有一些是经过计算的，圆弧上的点，从0开始到21，共22个点，其中11个点是xy平面上的，因为是做二维的仿真，xy平面上方的点与xy平面上的对应，只是z坐标有所不同，这里设置成0.5，即这个板的厚度为0.5m。
以及他们的连接方式，注意是逆时针方向。
教程上提供的图告诉我们这些点怎么成块：
另，这里涉及到曲线的设置方法。如果不另外设置，系统会默认成直线。看以下代码：
arc 就表示曲线（弧线）。另外，像上一篇文章，什么都不写就默认是simpleSpline（样条），还有是polyLine（多元曲线）。所以这里的arc只对于图中的圆弧线来定义的，其他未定义的线默认是直线。至于arc的用法：拿第一行举例：arc 0 5 （0.46 0.17 0） arc 后面的0 和5 都是点的标号，这个在vertices那里是定义好的（从上到下，从0开始）。后面的是插值点（interpolation point）的坐标值，因为arc是圆弧曲线，所以在原本的0和5两个点以外，只需要另外一个，就能定义一条圆弧。这里的点都是手动算的。
接下来看面的定义（boundary）：
因为这里是取四分之一个模型进行分析，所以左边（left）跟下边（down）都是设置成symmetry plane，意思是和它们之外还有接触的面，只是没画出来。而上面（up），右面（right）还有洞口（hole）都设成patch。关于z轴上下面都设置成empty，因为仿真是在二维平面上做的。从教材上po一个图，说明一下这些parameters的意思：
3. 设置初始值和边界条件（Boundary and initial conditions）
我们打开0/D（D即Displacement，位移）：
由dimension可知量纲为m；这里的left和down和上面一样，都是symmetryPlane。traction（拉力）施加在这个面上，意思是拉应力啦！大小是（1e4 0 0），即只在x方向（右边）有拉力，符合题意。压力设置成0。对于上方跟洞口，拉压力都设置成0。
在终端输入“paraFoam”，查看网格生成的情况。
4. 物理性质设置（Mechanical properties）
假定我们仿真用的是一块钢板（steel），那么物理性质如下：
性质（Property）从上倒下分别是密度（Density）、杨氏模量和泊松比。这个在constant/mechanicalProperties的文件里。
keywords 都是设定好的。
5. 热力学性质设置（Thermal properties)
从上到下分别是比热容、热传导率、热膨胀系数。文件在constant/thermalProperties.
6. Control
与上一篇文章类似，就不一一解说。
7. 离散、线性化（Discretisation schemes and linear-solver control）
这里我们要讲讲fvScheme。打开system/fvSchemes:
这里的设置很多！目前还在学习阶段，半懂不懂，希望能有大神来教教我！
8. 运行程序（Running the code）
solidDisplacementFoam > log &输入上述指令，意思是调用求解器（solver）去计算，然后将过程写在log上。
在log里面，可以看到收敛的信息：
9. 后处理（Post-processing)
在上一篇文章匆匆略过的部分，这一节讲一下。sigma指的是σ，在这里是板上的应力。运行下面一行代码，会帮你计算所设置的运行时间以内的所有网格的所有应力的信息，包括xy，xz，yz方向上。
postProcess -func "components(sigma)"打开paraview，查看应力的信息：
注意左下方那些栏都要打叉，不然看不到。
另外，也能查看板在收到应力时候的位移，在上面的sigma那里，选“D”：
我在blockMeshDict里面，将x，y方向上的网格都增加了一倍，即总体增加4倍。效果如下：
位移图像
应力图像
可以看到，精度是明显提高了！
还记得一开始说的那个解析解吗：
接下来我们将仿真所得的数值解与解析解进行比较，首先，制作一串sigma的数据
postProcess -func "singleGraph"然后在postProcess/singleGraph/100里找到line_sigmaxx.xy，进去一看：
怎么描画这些数据点呢？首先我们得在系统上安装gnuplot软件：
sudo apt-get update
sudo apt-get install gnuplot然后在命令行输入gnuplot，进入画画的状态：
如图，试了试sin(x)
在状态下，输入：
plot [0.5:2] [0:] "line_sigmaxx.xy",1e4*(1+(0.125/(x**2))+(0.09375/(x**4)))
如上图，实线为解析解，十字为数值解。
最后，我将deltaT （controlDict）里面的间隔时间从1s改到0.5s，时间精度提高了一倍，看看出来的效果如何：
好像没什么不一样。。。
时间关系，这次的博客先这样吧！
暂无评论内容