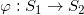清华笔记：计算共形几何讲义 （9）全纯微分

黎曼面上的微分形式的定义非常抽象，但是其背后具有非常丰富的几何内涵，对理解黎曼面的几何具有根本的重要性。（1,0）型的全纯微分，被称为是全纯1-形式（holomorphic 1-form）。全纯1-形式可以用于计算曲面的共形不变量，计算共形等价的曲面间的共形映射；（2,0）型的全纯微分，被称为是全纯二次微分（holomorphic quadratic differentials）。全纯二次微分可以用于计算曲面的叶状结构（foliation），非共形等价的曲面间最接近共形映射的极值映射；（-1,1）型的微分被称为是Beltrami 微分，固定两个黎曼面，则Beltrami微分控制了曲面间的微分同胚；全纯四次微分可以用于计算曲面的实射影结构。

  图4. 全纯1-形式的算法。

由此，我们可以计算曲面全纯一形式（holomorphic 1-form）群的基底，如图5所示。

图5. 亏格为2的曲面上全纯1-形式群的基底。

黎曼面上所有的全纯1-形式构成一个维复向量空间，通过复线性组合基底，我们可以遍历所有可能的全纯1-形式。根据实际应用的需要，我们从中挑选最优者，如图6所示。

图6. 黎曼面上的全纯1-形式构成复线性空间。

我们下面用亏格为一的曲面来解释如何使用全纯1-形式来计算几何问题。

图7. 亏格为一的曲面的共形模。

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1178631.html

上一篇：清华笔记：计算共形几何讲义 （8）狭缝映射（Slit Map）的存在性
下一篇：清华笔记：计算共形几何讲义 （10）纪念米尔扎哈尼——泰希米勒（Teichmuller）空间